A horizontal parabola features its own equations to find its parts; these are just a bit different when compared to a vertical parabola. The distance to the focus and directrix from the vertex in this case is horizontal, because they move along the axis of symmetry, which is a horizontal line. So, 1/(4a) is added to and subtracted from h.
The axis of symmetry is at y = v, and the vertex is still at (h, v).
The focus is directly to the left or right of the vertex, at the point (h + 1/4a),v)
The directrix is the same distance from the vertex as the focus in the opposite direction, at x = h – 1/4a.
Work with the equation to find the axis of symmetry, focal distance, and directrix.
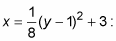
To find the axis of symmetry start with the vertex. The vertex of this parabola is (3, 1). The axis of symmetry is at y = v, so for this example, it is at y = 1.
For the equation given, a = 1/8, and so the focal distance is 2. Add this value to h to find the focus: (3 + 2, 1) or (5, 1).
To find the directrix, subtract the focal distance from Step 2 from h to find the equation of the directrix. Because this is a horizontal parabola and the axis of symmetry is horizontal, the directrix will be vertical. The equation of the directrix is x = 3 – 2 or x = 1.
Graph the parabola and label its parts.
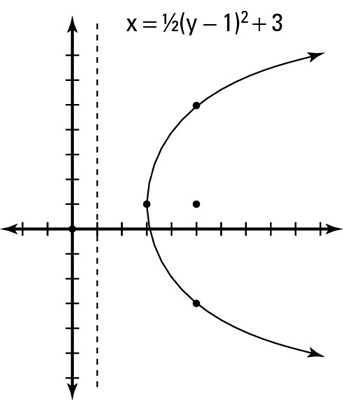
The figure shows you the graph and has all of the parts plotted for you. The focus lies inside the parabola, and the directrix is a vertical line 2 units from the vertex.
Square the variables in the equation.
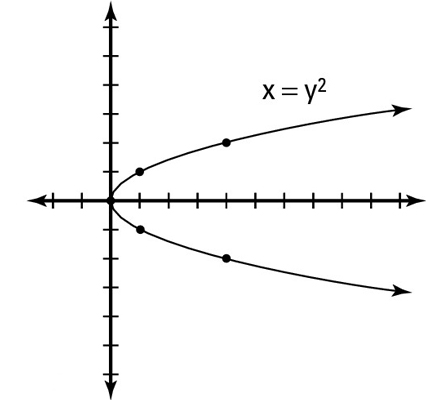
The squaring of the variables in the equation of the parabola determines where it opens: When y is squared and x is not, the axis of symmetry is horizontal and the parabola opens left or right. For example, x = y2 is a horizontal parabola; it’s shown in the figure.
Be aware of negative coefficients in parabolas. If the parabola is horizontal, a negative coefficient will make the parabola open to the left.






