The following proof introduces you to a new idea: adding a line or segment (called an auxiliary line) to a proof diagram to help you do the proof. Some proofs are impossible to solve until you add a line to the diagram.
Auxiliary lines often create congruent triangles, or they intersect existing lines at right angles. So if you’re stumped by a proof, see whether drawing an auxiliary line (or lines) could get you one of those things.
When you draw in an auxiliary line, just write something like
for the statement; then use the following postulate for the reason: “Two points determine a line (or ray or segment).”
Here’s an example proof:

You might come up with a game plan like the following:
Take a look at the givens. The only thing you can conclude from the single given is that the sides of GRAM are parallel (using the definition of a parallelogram). But it doesn’t seem like you can go anywhere from there. (For this proof, we’re assuming that you haven’t yet learned the properties of the parallelogram, one of which is that opposite sides are congruent.)
Jump to the end of the proof. What could be the justification for the final statement,

At this point, no justification seems possible, so put on your thinking cap.

Consider drawing an auxiliary line.

Show the triangles congruent.

That does it.
Here’s the formal proof:
Statement 1:
GRAM is a parallelogram.
Reason for statement 1: Given.
Statement 2:
Reason for statement 2: Two points determine a segment.
Statement 3:
Reason for statement 3: Definition of parallelogram.
Statement 4:
Reason for statement 4: If two parallel lines,
are cut by a transversal (segment RM), then alternate interior angles are congruent.
Statement 5:
Reason for statement 5: Definition of parallelogram.
Statement 6:
Reason for statement 6: Same as Reason 4, but this time
are the parallel lines.
Statement 7:
Reason for statement 7: Reflexive Property.
Statement 8:
Reason for statement 8: ASA (using lines 4, 7, and 6).
Statement 9:
Reason for statement 9: CPCTC.

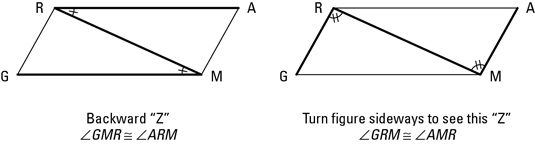
A good way to spot congruent alternate interior angles in a diagram is to look for pairs of so-called Z-angles. Look for a Z or backward Z — or a stretched-out Z or backward Z — as shown in the figures above and below. The angles in the crooks of the Z are congruent.