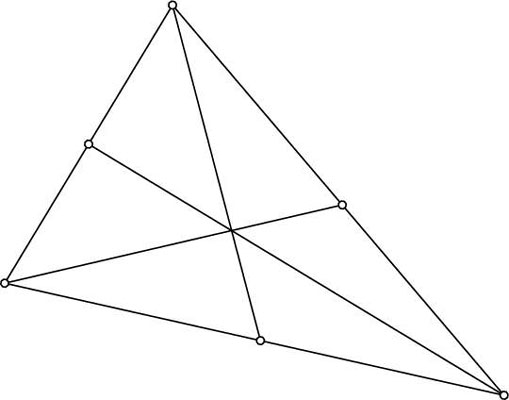
If you draw lines from each corner (or vertex) of a triangle to the midpoint of the opposite sides, then those three lines meet at a center, or centroid, of the triangle. The centroid is the triangle's center of gravity, where the triangle balances evenly. The coordinates of the centroid are also two-thirds of the way from each vertex along that segment.
The following image shows how the three lines drawn in the triangle all meet at the center.
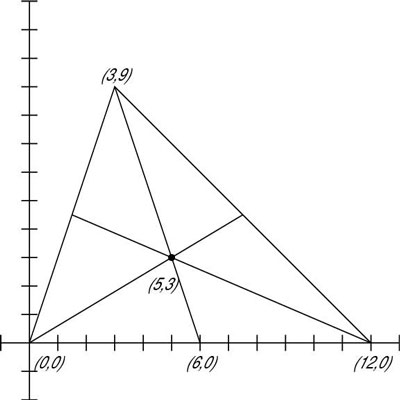
To find the centroid of a triangle, use the formula from the preceding section that locates a point two-thirds of the distance from the vertex to the midpoint of the opposite side.
For example, to find the centroid of a triangle with vertices at (0,0), (12,0) and (3,9), first find the midpoint of one of the sides. The most convenient side is the bottom, because it lies along the x-axis. The coordinates of that midpoint are (6,0). Then find the point that sits two-thirds of the way from the opposite vertex, (3,9):
Replace x1, x2, y1, and y2 with their respective values. Replace k with 2/3.

Simplify the computation to get the point.

In this example, the centroid is the point (5,3).