The most important derivatives and antiderivatives to know
The table below shows you how to differentiate and integrate 18 of the most common functions. As you can see, integration reverses differentiation, returning the function to its original state, up to a constant C.

The Riemann Sum Formula for the definite integral
The Riemann Sum formula provides a precise definition of the definite integral as the limit of an infinite series. The Riemann Sum formula is as follows:
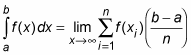
Below are the steps for approximating an integral using six rectangles:
![]()
-
Increase the number of rectangles (n) to create a better approximation:

-
Simplify this formula by factoring out w from each term:

-
Use the summation symbol to make this formula even more compact:

The value w is the width of each rectangle:

Each h value is the height of a different rectangle:

So here is the Riemann Sum formula for approximating an integral using n rectangles:

-
For a better approximation, use the limit

-
to allow the number of rectangles to approach infinity:

Integration by parts with the DI-agonal method
The DI-agonal method is basically integration by parts with a chart that helps you organize information. This method is especially useful when you need to integrate by parts more than once to solve a problem. Use the following table for integration by parts using the DI-agonal method:

The Sum Rule, the Constant Multiple Rule, and the Power Rule for integration
When you perform integration, there are three important rules that you need to know: the Sum Rule, the Constant Multiple Rule, and the Power Rule.
The Sum Rule for Integration tells you that it’s okay to integrate long expressions term by term. Here it is formally:
![]()
The Constant Multiple Rule for Integration tells you that it’s okay to move a constant outside of an integral before you integrate. Here it is expressed in symbols:
![]()
The Power Rule for Integration allows you to integrate any real power of x (except -1). Here’s the Power Rule expressed formally:
where n ≠ -1
![]()
How to solve integrals with variable substitution
In Calculus, you can use variable substitution to evaluate a complex integral. Variable substitution allows you to integrate when the Sum Rule, Constant Multiple Rule, and Power Rule don’t work.
-
Declare a variable u, set it equal to an algebraic expression that appears in the integral, and then substitute u for this expression in the integral.
-
Differentiate u to find

and then isolate all x variables on one side of the equal sign.
-
Make another substitution to change dx and all other occurrences of x in the integral to an expression that includes du.
-
Integrate by using u as your new variable of integration.
-
Express this answer in terms of x.
How to Use integration by parts
When doing Calculus, the formula for integration by parts gives you the option to break down the product of two functions to its factors and integrate it in an altered form. To use integration by parts in Calculus, follow these steps:
-
Decompose the entire integral (including dx) into two factors.
-
Let the factor without dx equal u and the factor with dx equal dv.
-
Differentiate u to find du, and integrate dv to find v.
-
Use the formula:

-
Evaluate the right side of this equation to solve the integral.
How to solve compound functions where the inner function is ax + b
Some integrals of compound functions f (g(x)) are easy to do quickly in Calculus. These include compound functions for which you know how to integrate the outer function f, and the inner function g(x) is of the form ax + b — that is, it differentiates to a constant.
Here are some examples:

Solve compound functions where the inner function is ax
When figuring Calculus problems, some integrals of compound functions f (g(x)) are easy to do quickly. These include compound functions for which you know how to integrate the outer function f, and the inner function g(x) is of the form ax — that is, it differentiates to a constant.
Here are some examples:






