Graph an Area Where Inequalities Overlap

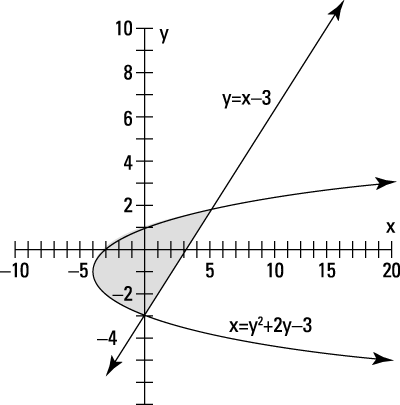
You can find the solution of a system of inequalities involving a line and a curve (such as a parabola), two curves, or any other such combination.

You do this by graphing the individual equations, determining which side to shade for each curve, and identifying where the equations share the shading. For example, to solve the system

make your way through the following steps:

1. Graph the line y = x – 3 and determine which side of the line to shade by checking a test point (a random point that's clearly on one side or the other) to see if it satisfies the inequality.

   If the point satisfies the inequality, you shade that side. In this case, you can use the test point (0, 0), which is clearly above and to the left of the line. When you put the coordinate (0, 0) in the inequality

   

   you get

   

   Yes, 0 is greater than –3, so the test point is in the area that you need to shade — above the line.

2. Graph the parabola x = y² + 2y – 3 and use a test point to see whether you need to shade inside the parabola or outside the parabola.

   Again, the point (0, 0) is handy. Test the point in the inequality for the parabola,

   

   You find

   

   which is true. So, the point (0, 0) falls in the area you need to shade — inside the parabola.

3. Determine where the two shaded areas overlap to find your solution to the system of inequalities.

   The two shaded areas overlap where the inside of the parabola and area above the line intersect.

The figure shows the line and parabola corresponding to the inequalities. The shaded area indicates the solution — where the two inequalities overlap.

A parabola and line outline a solution wedge for the inequalities.