Multiplying and dividing positive and negative numbers is a simple operation with two numbers. With three or more, it is also straightforward, but you use the Even-Odd Rule.
With two numbers, the rules for multiplying and dividing positive and negative numbers are not only simple, but they’re also the same for both operations:
When multiplying or dividing two numbers, if the two signs are the same, the result is positive, and if the two signs are different, the result is negative.
When multiplying and dividing more than two numbers, count the number of negatives to determine the final sign: An even number of negatives means the result is positive, and an odd number of negatives means the result is negative.
You multiply and divide positive and negative numbers “as usual” except for the positive and negative signs. So ignore the signs and multiply or divide. Then, if you're dealing with two numbers, the result is positive if the signs of both numbers are the same, and the result is negative if the signs of both numbers are different.
Check out the following examples:
So, 8 multiplied by 2 is 16, and because the signs of both numbers are different, the answer is negative, –16.
So, 5 multiplied by 11 is 55, and because the signs of both numbers are the same, the result is positive, +55.
So, 24 divided by 3 is 8, and because both numbers have different signs, the result is negative, –8.
So, 30 divided by 2 is 15, and because both numbers have the same signs, the answer is positive, +15.
When multiplying and dividing more than two positive and negative numbers, use the Even-Odd Rule: Count the number of negative signs — if you have an even number of negatives, the result is positive, but if you have an odd number of negatives, the result is negative.
The following examples show you how to use the Even-Odd Rule:
This problem has just one negative sign. Because one is an odd number, the answer is negative.
Two negative signs mean a positive answer because two is an even number.
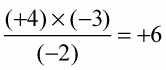
An even number of negative signs means a positive answer.
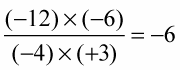
Three negative signs mean a negative answer.






