Functions can have many classifications or names, depending on the situation and what you want to do with them. One very important classification is deciding whether a function is one-to-one. You can do this using graphing techniques called vertical and horizontal line tests.
A function is one-to-one if it has exactly one output value for every input value and exactly one input value for every output value. Formally, you write this definition as follows:
If f (x1) = f (x2), then x1 = x2
In simple terms, if the two output values of a function are the same, then the two input values must also be the same.
You can determine which functions are one-to-one and which are violators by sleuthing (guessing and trying), using algebraic techniques, and graphing. Most mathematicians prefer the graphing technique because it gives you a nice, visual answer. The basic graphing technique is the horizontal line test. But, to better understand this test, you need to meet its partner, the vertical line test.
Identify a function with the vertical line test
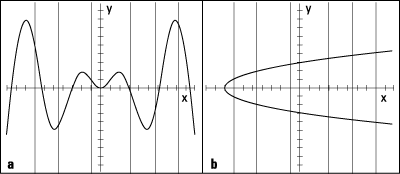
The graph of a function always passes the vertical line test. The test stipulates that any vertical line drawn through the graph of the function passes through that function no more than once. This is a visual illustration that only one y value (output) exists for every x value (input), a rule of functions. Figure a shows a function that passes the vertical line test, and Figure b contains a curve that isn't a function and therefore flunks the vertical line test.
Identify a function with the horizontal line test
All functions pass the vertical line test, but only one-to-one functions pass the horizontal line test. With this test, you can see if any horizontal line drawn through the graph cuts through the function more than one time. If the line passes through the function more than once, the function fails the test and therefore isn't a one-to-one function. Figure a shows a function that passes the horizontal line test, and Figure b shows a function that flunks it.
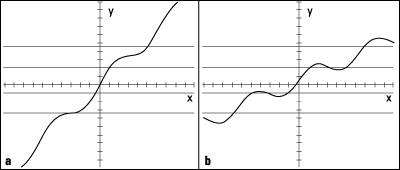
Both graphs in the figure are functions, however, so they both pass the vertical line test.






