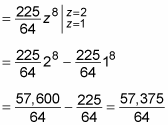Triple integrals are usually definite integrals, so evaluating them results in a real number. Evaluating triple integrals is similar to evaluating nested functions: You work from the inside out.
Triple integrals look scary, but if you take them step by step, they’re no more difficult than regular integrals. You start in the center and work your way out. For example:
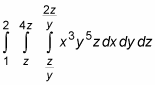
Begin by separating the two inner integrals:
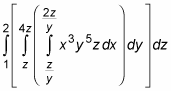
Your plan of attack is to evaluate the integral in the brackets first, and then the integral in the braces, and finally the outer integral. First things first:
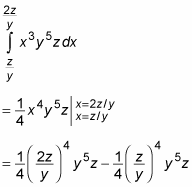
Notice that plugging in values for x results in an expression in terms of y and z. Now simplify this expression to make it easier to work with:
Plug this solution back in to replace the bracketed integral:
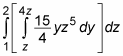
One integral down, two to go. Now focus on the integral inside the braces. This time, the integration variable is y:
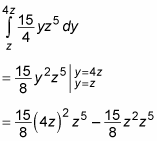
Again, simplify before proceeding:
Plug this result back into the integral as follows:
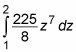
Now evaluate this integral: