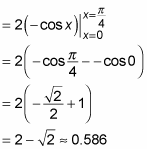Sometimes, a single geometric area is described by more than one function. For example, suppose that you want to find the shaded area shown in the following figure, the area under y = sin x and y = cos x from 0 to Π/2:
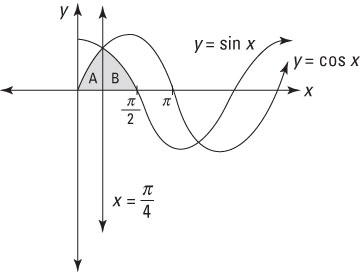
The first thing to notice is that the shaded area isn’t under a single function, so you can’t expect to use a single integral to find it. Instead, the region labeled A is under y = sin x and the region labeled B is under y = cos x. First, set up an integral to find the area of both of these regions:
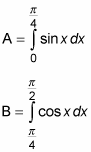
Now set up an equation to find their combined area:
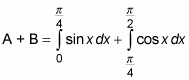
At this point, you can evaluate each of these integrals separately. But there’s an easier way.
Because region A and region B are symmetrical, they have the same area. So you can find their combined area by doubling the area of a single region:
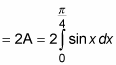
Here, region A is doubled because the integral limits of integration are easier, but doubling region B also works. Now integrate to find your answer: