Finding the volume of a prism or cylinder is pretty straightforward. But what if you need to find the volume of a shape like the one shown here? In this case, slicing parallel to the base always results in the same shape — a circle — but the area may differ. That is, the solid has similar cross sections rather than congruent ones.
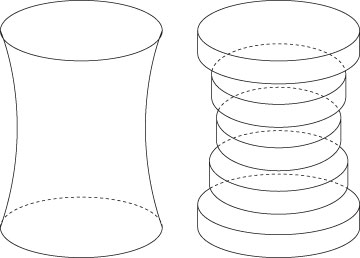
You can estimate this volume by slicing the solid into numerous cylinders, finding the volume of each cylinder by using the formula for constant-height solids, and adding these separate volumes. Of course, making more slices improves your estimate. And, as you may already suspect, taking the limit of a sum of these slices as the number of slices increases without bound gives you the exact volume of the solid.
Hmmm . . . this is beginning to sound like a job for calculus. Specifically, you can use the meat-slicer method, which works well for measuring solids that have similar cross sections.
Here’s the plan:
Find an expression that represents the area of a random cross section of the solid in terms of x.
Use this expression to build a definite integral (in terms of dx) that represents the volume of the solid.
Evaluate this integral.
When a problem asks you to find the volume of a solid, look at the picture of this solid and figure out how to slice it up so that all the cross sections are similar. This is a good first step in understanding the problem so that you can solve it.






