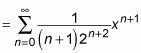Because power series resemble polynomials, they’re simple to integrate using a simple three-step process that uses the Sum Rule, Constant Multiple Rule, and Power Rule.
For example, take a look at the following integral:
At first glance, this integral of a series may look scary. But to give it a chance to show its softer side, you can expand the series out as follows:
Now you can apply the three steps for integrating polynomials to evaluate this integral:
Use the Sum Rule to integrate the series term by term:

Use the Constant Multiple Rule to move each coefficient outside its respective integral:

Use the Power Rule to evaluate each integral:

Notice that this result is another power series, which you can turn back into sigma notation: