How to Integrate Odd Powers of Sines and Cosines

You can integrate any function of the form sin^m x cosⁿ x when m is odd, for any real value of n. For this procedure, keep in mind the handy trig identity sin²x + cos²x = 1. For example, here’s how you integrate

1. Peel off a sin x and place it next to the dx:

   

2. Apply the trig identity sin²x = 1 – cos²x to express the rest of the sines in the function as cosines:

   

3. Use the variable substitution u = cos x and du = –sin x dx:

   

Now that you have the function in terms of powers of u, the worst is over. You can expand the function out, turning it into a polynomial. This is just algebra:

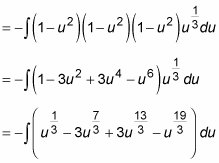
To continue, use the Sum Rule and Constant Multiple Rule to separate this into four integrals. Don’t forget to distribute that minus sign to all four integrals!

At this point, you can evaluate each integral separately using the Power Rule:

Finally, use u = cos x to reverse the variable substitution:

Notice that when you substitute back in terms of x, the power goes next to the cos rather than next to the x, because you’re raising the entire function cos x to a power.

Similarly, you integrate any function of the form sin^m x cosⁿ x when n is odd, for any real value of m. These steps are practically the same as those in the previous example. For instance, here’s how you integrate sin^–4x cos⁹x:

1. Peel off a cos x and place it next to the dx:

   

2. Apply the trig identity cos²x = 1 – sin²x to express the rest of the cosines in the function as sines:

   

3. Use the variable substitution u = sin x and du = cos x dx:

   

At this point, you can distribute the function and express it as a sum of powers of u.