![]()
This formula works just fine, but it doesn’t give you insight into how to solve similar problems; it works only for pyramids. The meat-slicer method, however, provides an approach to the problem that you can generalize to use for many other types of solids.
 x-axis of a graph."/>
x-axis of a graph."/>
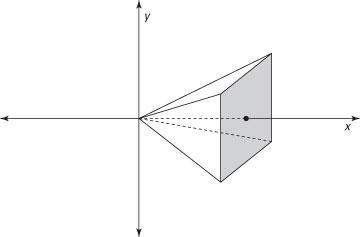
To find the exact volume of the pyramid, here’s what you do:
-
Find an expression that represents the area of a random cross section of the pyramid in terms of x.
At x = 1, the cross section is 22 = 4. At x = 2, it’s 42 = 16. And at x = 3, it’s 62 = 36. So generally speaking, the area of the cross section is:
A = (2x)2 = 4x2
-
Use this expression to build a definite integral that represents the volume of the pyramid.
In this case, the limits of integration are 0 and 3, so:

-
Evaluate this integral:







