You can use your knowledge of geometric constructions (as well as a compass and straight edge) to create congruent angles. The following practice questions test your construction skills.
If you're drawing two arcs for a construction, make sure you keep the width of the compass (or radii of the circles) consistent.
Practice questions
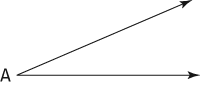
Use the above figure to construct

an angle congruent to angle A.

Use the above figure to construct

a triangle congruent to triangle BCA.
Answers and explanations
1.Here is the solution:

Use a straight edge to draw a ray with endpoint D. Place the compass point on A, and with any width, draw an arc intersecting the angle at two points.

Using the same width, place the compass point at D and make an arc.

Using the compass, measure the distance between B and C. Keeping that compass width, place the compass point at E and draw an arc. Connect the point where the arcs intersect to D.

2.Here is the solution:

Place the compass point at B and measure the length of

Draw Point D on your paper. Keeping the length of

place the compass point on D and draw an arc. Place a point on the arc and label it E.

Use your compass to measure the length of

Keeping that compass width, place the compass point at D and draw an arc where the third vertex would be located.

Use your compass to measure the length of

Keeping that compass width, place the compass point at E and draw an arc where the third vertex would be. Name the point where the arcs intersect F. Connect the three vertices of the triangle.







