You can prove that triangles are similar using the SAS~ (Side-Angle-Side) method. SAS~ states that if two sides of one triangle are proportional to two sides of another triangle and the included angles are congruent, then the triangles are congruent. (Given two sides of a triangle, the included angle is the angle formed by the two sides.)
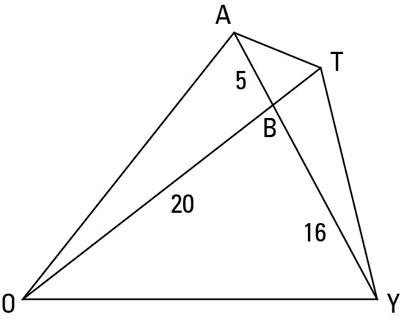
Try using the SAS~ method to do the following proof:
Game Plan: Your thinking might go like this. You have one pair of congruent angles, the vertical angles ABT and OBY. But because it doesn’t look like you can get another pair of congruent angles, the AA (Angle-Angle) approach is out. What other method can you try?
You’re given side lengths in the figure, so the combination of angles and sides should make you think of SAS~.

So you begin solving the problem by figuring out the length of segment BT.
Thus, you can set up this proportion:

This checks. You’re done.






