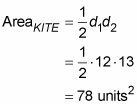The Chord-Chord Power Theorem was named for the fact that it uses a chord and — can you guess? — another chord!
Chord-Chord Power Theorem: If two chords of a circle intersect, then the product of the measures of the parts of one chord is equal to the product of the measures of the parts of the other chord. (Whew, what a mouthful!)
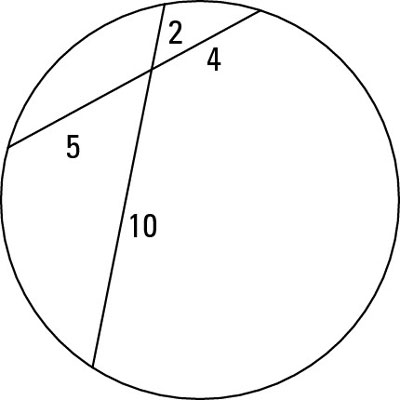
For example, in the above figure,
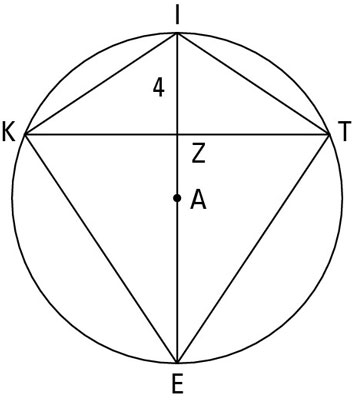
Using the figure above, try out your power-theorem skills on the following problem:

To get the area of a kite, you need to know the lengths of its diagonals. This kite’s diagonals are two chords that cross each other, so you can use the Chord-Chord Power Theorem.

Then you see that ZE must be 13 – 4, or 9. Now you have two of the lengths, IZ = 4 and ZE = 9, for the segments you use in the theorem:
(KZ)(ZT) = (IZ)(ZE)
Plug everything into the chord-chord equation:
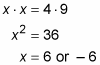
You can obviously reject –6 as a length, so x is 6.
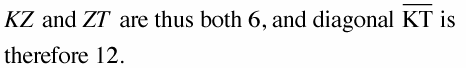
You’ve already figured out that the length of the other diagonal is 13, so now you finish with the kite area formula: