In geometry, you may be given specific information about a triangle and in turn be asked to prove something specific about it. The following example requires that you use the SAS property to prove that a triangle is congruent.
Practice questions
Use the following figure to answer each question.
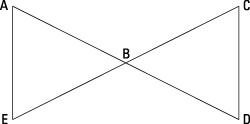
Given
bisect each other at B.
Prove:
The following questions ask you to fill in the blanks in the table.

What is the reason for Statement 2?
What is the statement for Reason 3?
What is the reason for Statement 4?
What is the reason for Statement 5?
What is the reason for Statement 6?
Answers and explanations
A bisector divides a segment into two congruent segments.
A bisector divides a segment or angle into two congruent parts, so

-

are vertical angles.
Intersecting lines form vertical angles.
If two angles are vertical angles, then they're congruent.
Vertical angles are congruent, so

SAS
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent by SAS (side-angle-side). Therefore,

CPCTC
Corresponding parts of congruent triangles are congruent to each other, so







