How to Solve a Triangle When You Know Two Consecutive Side Lengths (SSA)

In some trig problems, you may be given two sides of a triangle and an angle that isn't between them, which is the classic case of SSA, or Side-Side-Angle. In this scenario, you may have one solution, two solutions, or no solutions.

The best approach is to always assume that you'll find two solutions, because remembering all the rules that determine the number of solutions probably will take up far too much time and energy. If you treat every SSA problem as if it has two solutions until you gather enough information to prove otherwise, you'll be twice as likely to find all the appropriate solutions.

Gaining some experience with solving a triangle that has more than one solution is helpful. The first set of solutions that you find in such a situation always contains an acute triangle. The second set of solutions always contains an obtuse triangle.

Two possible representations of an SSA triangle.

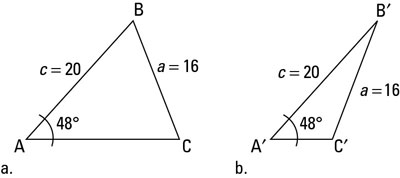
For example, say you're given a = 16, c = 20, and

Figure a shows you what the picture may look like. However, couldn't the triangle also look like Figure b? Both situations follow the constraints of the given information of the triangle. If you start by drawing your picture with the given angle, the side next to the angle has a length of 20, and the side across from the angle is 16 units long. The triangle could be formed two different ways. Angle C could be an acute angle or an obtuse angle; the given information isn't restrictive enough to tell you which one it is. Therefore, you have to find both sets of solutions.

Solving this triangle by using the following steps gives you the two possible solutions shown in the figure. Because you have two missing angles, you need to find one of them first:

1. Fill in the Law of Sines formula with what you know.

   Given that the formula for the Law of Sines looks like this:

   

   the formula here sets up like this:

   

2. Set two fractions equal to each other so that you have only one unknown.

   Say you decide to solve for angle C. In this case, you set the first and third fractions equal to each other, and so you have this equation:

   

3. Cross multiply and isolate the sine function.

   This step gives you

   

   To isolate the sine function, you divide by 16:

   

4. Take the inverse sine of both sides.

   

   The right-hand side goes right into your handy calculator to give you

   

5. Determine the third angle.

   You know that

   

6. Plug the final angle back into the Law of Sines formula to find the third side.

   This step gives you

   

   Finally, you can solve:

   

Of course, this solution to the triangle isn't the only one. Refer to Step 4, where you solved for angle C, and then look at this figure:

The two possible triangles overlapping

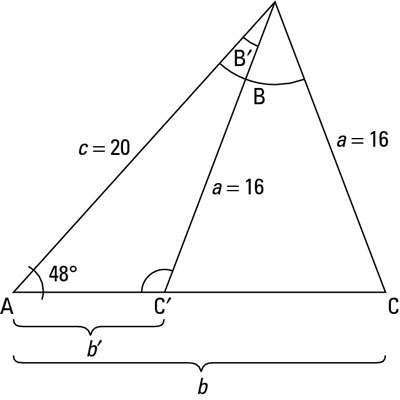
Triangle ABC is the solution that you solved for in these steps. Triangle AB'C' is the second set of solutions you must look for. A certain trig identity isn't used in solving or simplifying trig expressions because it isn't helpful for those, but it is useful for solving triangles. This identity says that

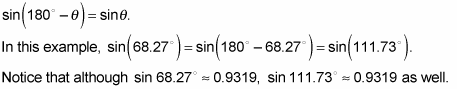
However, if you plug sin^–1(0.9319) into your calculator to solve for theta, 68.27 degrees is the only solution you get. Subtracting this value from 180 degrees gives you the other ambiguous solution for angle C, which is usually denoted as angle C' so you don't confuse it with the first solution.

The following steps build on these actions so you can find all the solutions for this SSA problem:

1. Use the trig identity

   

2. to find the second angle of the second triangle.

   Because

   

   subtract this value from 180 degrees to find that

   

3. Find the measure of the third angle.

   

   because the three angles must add to 180 degrees.

4. Plug these angle values into the Law of Sines formula.

   

5. Set one fraction with an unknown numerator and the fraction with a known numerator equal to each other in the formula.

   You need to find b'. Set the first fraction equal to the second:

   

6. Cross multiply to solve for the variable.

   

   Isolate b' to get this solution:

   

7. List all the answers to the two triangles (see the previous numbered list).

   Originally, you were given that a = 16, c = 20, and angle A = 48 degrees. The answers that you found are as follows:

   • First triangle.

     

   • Second triangle.