45-45-90 degree triangles
All 45-45-90-degree triangles (also known as 45ers) have sides that are in a unique ratio. The two legs are the exact same length, and the hypotenuse is that length times the square root of 2. The figure shows the ratio. If you look at the 45er triangle in radians, you have![]()
Either way, it's still the same ratio.

-
Type 1: You're given one leg.
Because you know both legs are equal, you know the length of both the legs. You can find the hypotenuse by multiplying this length by the square root of 2.
-
Type 2: You're given the hypotenuse.
Divide the hypotenuse by the square root of 2 to find the legs (which are equal).

![]()
You must now rationalize the denominator to get
![]()
which is the measure of each side of the square.
30-60-90 degree triangles
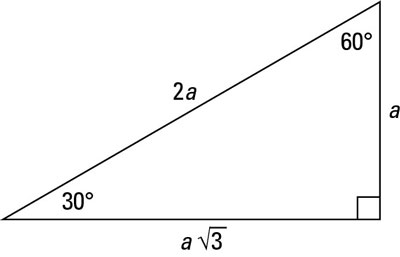
The 30-60-90 degree triangle is in the shape of half an equilateral triangle, cut straight down the middle along its altitude. It has angles of 30°, 60°, and 90°. In any 30-60-90 triangle, you see the following: The shortest leg is across from the 30-degree angle, the length of the hypotenuse is always double the length of the shortest leg, you can find the long leg by multiplying the short leg by the square root of 3.Note: The hypotenuse is the longest side in a right triangle, which is different from the long leg. The long leg is the leg opposite the 60-degree angle.
Two of the most common right triangles are 30-60-90 and the 45-45-90 degree triangles. All 30-60-90 triangles, have sides with the same basic ratio. If you look at the 30–60–90-degree triangle in radians, it translates to the following:
![]()
The figure illustrates the ratio of the sides for the 30-60-90-degree triangle.
-
Type 1: You know the short leg (the side across from the 30-degree angle). Double its length to find the hypotenuse. You can multiply the short side by the square root of 3 to find the long leg.
-
Type 2: You know the hypotenuse. Divide the hypotenuse by 2 to find the short side. Multiply this answer by the square root of 3 to find the long leg.
-
Type 3: You know the long leg (the side across from the 60-degree angle). Divide this side by the square root of 3 to find the short side. Double that figure to find the hypotenuse.
 Finding the other sides of a 30-60-90 triangle when you know the hypotenuse
Finding the other sides of a 30-60-90 triangle when you know the hypotenuse
Because you have the hypotenuse TR = 14, you can divide by 2 to get the short side: RI = 7. Now you multiply this length by the square root of 3 to get the long side:
![]()






