When designing a study, the sample size is an important consideration because the larger the sample size, the more data you have and the more precise your results will be (assuming high-quality data). If you know the level of precision you want (that is, your desired margin of error), you can calculate the sample size needed to achieve it.
To find the sample size needed to estimate a population mean,
or a population proportion (p), use the following formula:
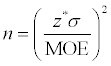
where z* is the critical value for the confidence level you need; MOE represents the desired margin of error; and
represents the population standard deviation.
If
σ is unknown,
When looking for

estimate
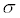
with the sample standard deviation, s, from a pilot study.
When looking for p, estimate
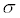
with p0(1 – p0), where p0 is some initial guess (usually 0.50) at p.






