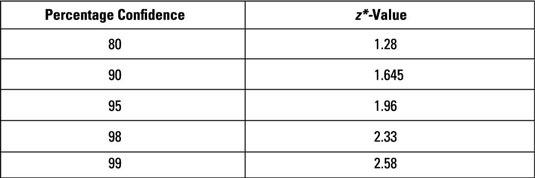
The three practice questions here can help you achieve an understanding of the relationship between values of z and the confidence level needed for a margin of error. Use the following table to find the appropriate z*-value for the confidence levels given except where noted.
Sample questions
The Z-table and the preceding table are related but not the same. To see the connection, find the z*-value that you need for a 95% confidence interval by using the Z-table:
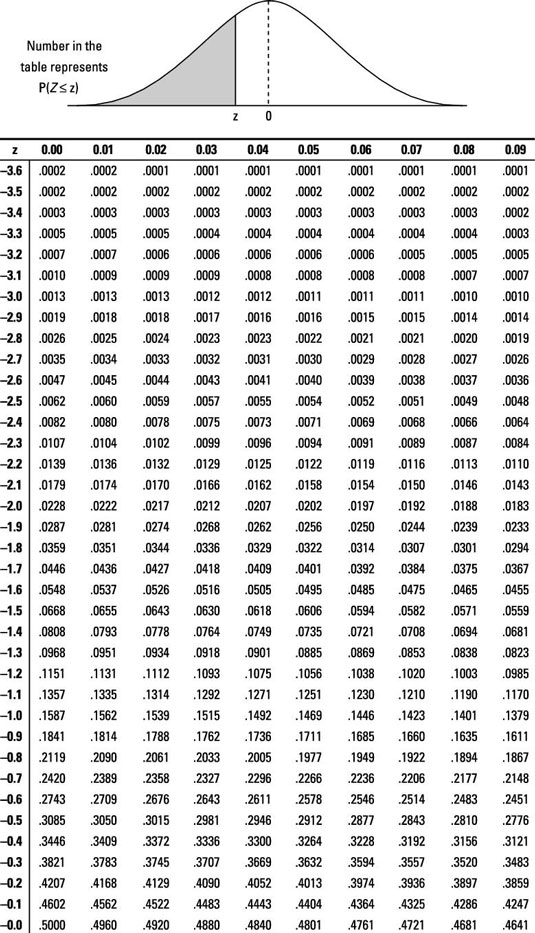
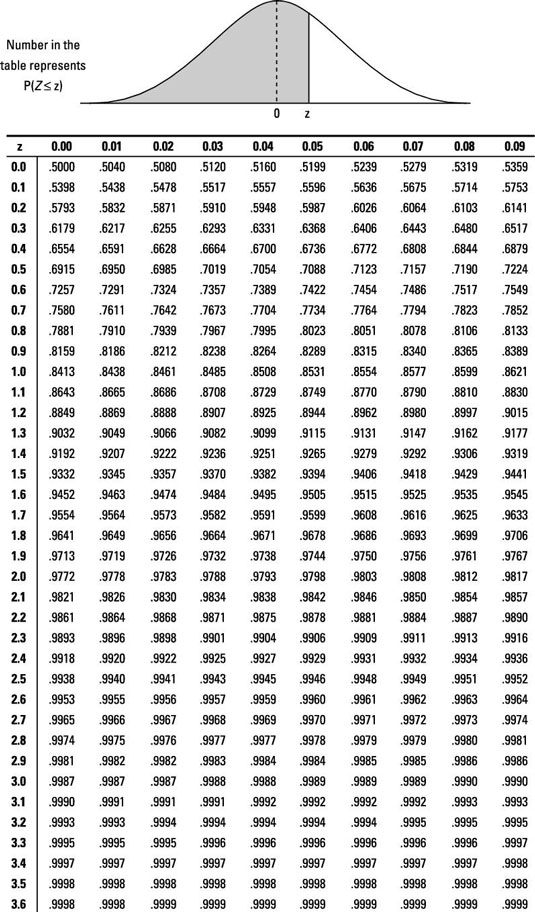
Answer: 1.96
First off, if you look at the z*-table, you see that the number you need for z* for a 95% confidence interval is 1.96. However, when you look up 1.96 on the Z-table, you get a probability of 0.975. Why?
In a nutshell, the Z-table shows only the probability below a certain z-value, and you want the probability between two z-values, –z and z. If 95% of the values must lie between –z and z, you expand this idea to notice that a combined 5% of the values lie above z and below –z. So 2.5% of the values lie above z, and 2.5% of the values lie below –z.
To get the total area below this z-value, take the 95% between –z and z plus the 2.5% below –z, and you get 97.5%. That's the z-value with 97.5% area below it. It's also the number with 95% lying between two z-values, –z and z.
To avoid all these extra steps and headaches, the z*-table has already done this conversion for you. So when you look up 1.96, you automatically find 95% (not 97.5%).
What is the z*-value for a 99% confidence level?
Answer: 2.58
The z*-table shows the answer: A 99% confidence level has a z*-value of 2.58.
What is the z*-value for a confidence level of 80%?
Answer: 1.28
The z*-table shows the answer: An 80% confidence level has a z*-value of 1.28.
If you need more practice on this and other topics from your statistics course, visit 1,001 Statistics Practice Problems For Dummies to purchase online access to 1,001 statistics practice problems! We can help you track your performance, see where you need to study, and create customized problem sets to master your stats skills.






