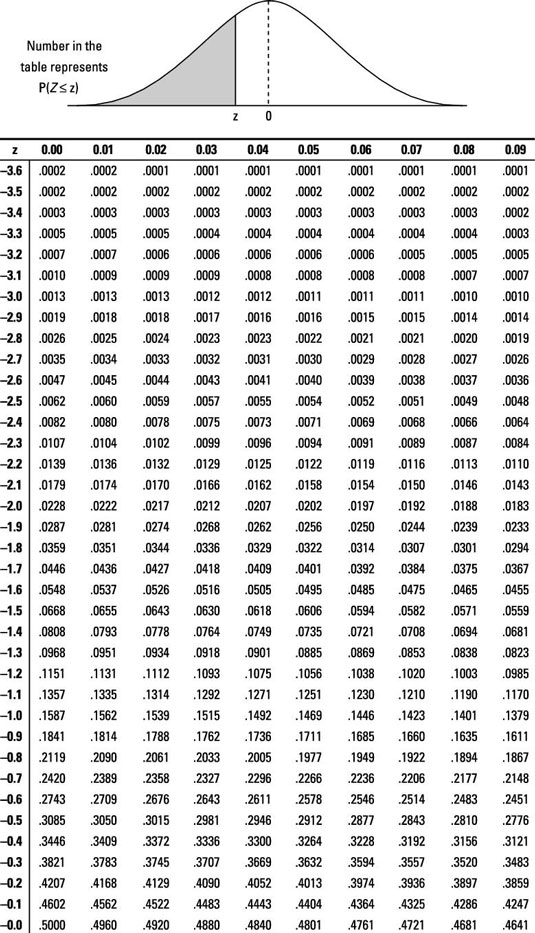
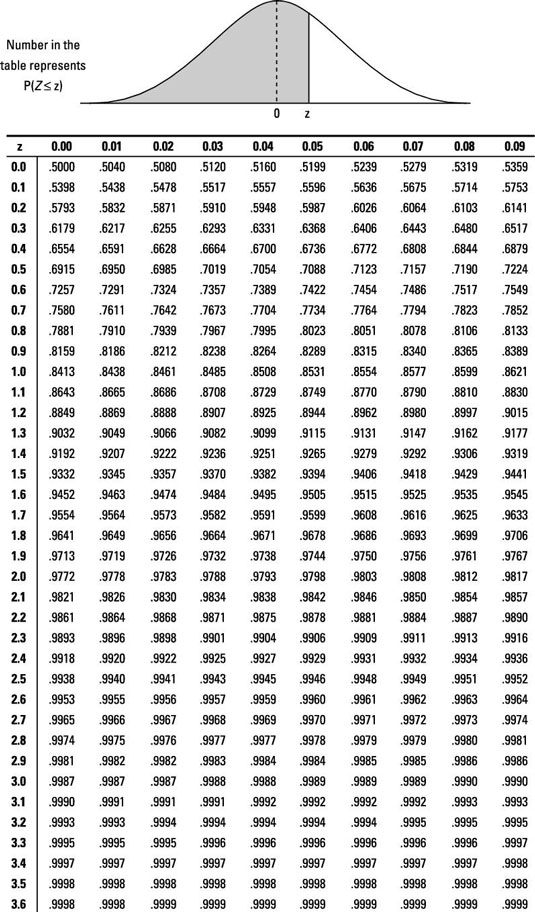
Z Score Table Sample Problems
Use these sample z-score math problems to help you learn the z-score formula.-
What is P (Z ≤ 1.5) ?
Answer: 0.9332
To find the answer using the z-table, find where the row for 1.5 intersects with the column for 0.00; this value is 0.9332. The z-table shows only "less than" probabilities so it gives you exactly what you need for this question. Note: No probability is exactly at one single point, so:
P (Z ≤ 1.5) = P (Z < 1.5) -
What is P (Z ≥ 1.5) ?
Answer: 0.0668
Use the z-table to find where the row for 1.5 intersects with the column for 0.00, which is 0.9332. Because the z-table gives you only "less than" probabilities, subtract P(Z < 1.5) from 1 (remember that the total probability for the normal distribution is 1.00, or 100%):
P (Z ≥ 1.5) = 1 – P (Z < 1.5)= 1 – 0.9332 = 0.0668
-
What is P (–0.5 ≤ Z ≤ 1.0) ?
Answer: 0.5328
To find the probability that Z is between two values, use the z-table to find the probabilities corresponding to each z-value, and then find the difference between the probabilities.
Here, you want the probability that Z is between –0.5 and 1.0. First, use the z-table to find the value where the row for –0.5 intersects with the column for 0.00, which is 0.3085. Then, find the value where the row for 1.0 intersects with the column for 0.00, which is 0.8413.
Because the z-table gives you only "less than" probabilities, find the difference between the probability less than 1.0 and the probability less than –0.5:
P (–0.5 ≤ Z ≤ 1.0) = P (Z ≤ 1.0) – P (Z ≤ –0.50)= 0.8413 – 0.3085 = 0.5328
-
What is P (–1.0 ≤ Z ≤ 1.0) ?
Answer: 0.6826
To find the probability that Z is between two values, use the z-table to find the probabilities corresponding to each z-value, and then find the difference between the probabilities.
Here, you want the probability that Z is between –1.0 and 1.0. First, use the z-table to find the value where the row for –1.0 intersects with 0.00, which is 0.1587. Then, find the value where the row for 1.0 intersects with the column for 0.00, which is 0.8413.
Because the z-table gives you only "less than" probabilities, find the difference between probability less than 1.0 and the probability less than –1.0:
P (–1.0 ≤ Z ≤ 1.0) = P (Z ≤ 1.0) – P (Z ≤ –1.0)= 0.8413 – 0.1587 = 0.6826






