The sine values for 30, 150, 210, and 330 degrees are 1/2, 1/2, –1/2, and –1/2, respectively. All these multiples of 30 degrees have a sin whose absolute value of 1/2 . The following rule and figure help you determine whether a trig-function value is positive or negative. First, note that each quadrant in the figure is labeled with a letter. The letters aren’t random; they stand for trig functions.
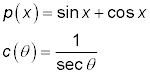
Reading around the quadrants, starting with QI and going counterclockwise, the rule goes like this: If the terminal side of the angle is in the quadrant with letter
A: All functions are positive.
S: Sine and its reciprocal, cosecant, are positive.
T: Tangent and its reciprocal, cotangent, are positive.
C: Cosine and its reciprocal, secant, are positive.
In QII, only sine and cosecant are positive. All the other function values for angles in this quadrant are negative — and the rule continues in like fashion for the other quadrants.
Remember this rule: “All Students Take Calculus.” If math is already giving you nightmares, maybe you’d prefer “Any Snake Teases Chickens” or “Apple Sauce Turns Colors.” Make up your own! Have at it!





