One way to describe the middle of a circle is to identify the centroid. This middle-point is the center of gravity, where you could balance the triangle and spin it around.
When you graph a circle, triangle, or line segment by using coordinate axes, then you can name these middle points with a pair of x- and y-coordinates. All you need to find these middles are the coordinates of some crucial other points on the respective figures.
If the endpoints of one diameter of a circle are (x1,y1) and (x2,y2), then the center of the circle has the coordinates
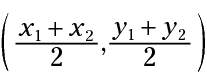
You probably noticed that the center of a circle is the same as the diameter's midpoint. The center of the circle separates the diameter into two equal segments called radii (plural for radius).
The figure shows a circle with a diameter whose endpoints are (7,4) and (–1,–2). The center of the circle is at (3,1). The coordinates for the center were found by using the formula for the midpoint of a segment:
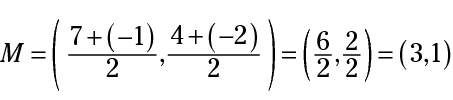
You find the length of the diameter by using the distance formula:
For the circle shown, the diameter is 10 units long.
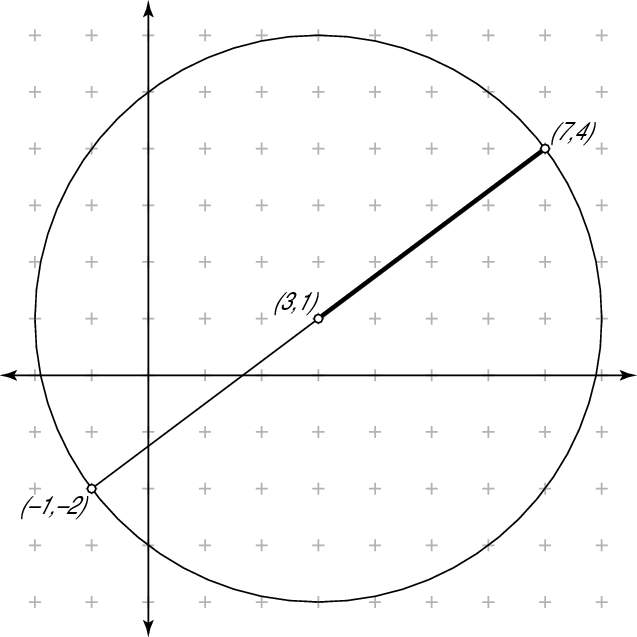
Next, you find the length of one of the radii. Either will do — they're the same length. In this example, figure the radius length from the center of the circle (3,1) to the endpoint of the diameter (7,4):
The radius is 5 units long. But, of course, you expected this answer, because by definition, the radius is half the length of the diameter.





