You can find the area of a triangle using Heron's Formula. Heron's Formula is especially helpful when you have access to the measures of the three sides of a triangle but can't draw a perpendicular height or don't have a protractor for measuring an angle.
Consider the situation where you have a large ball of string that's 100 yards long and you're told to mark off a triangular area — with the string as the marker for the border of the area. You walk 40 yards in one direction, take a turn, and walk another 25 yards; then you head back to where you started and use up that last 35 yards of string.
How large an area have you created?
Heron's Formula reads:
where a, b, and c are the lengths of the sides of the triangle and s is the semi-perimeter (half the perimeter).
In the case of your triangle and the string, the perimeter is 40 + 25 + 35 = 100 yards. Half that is 50, so the formula now reads:
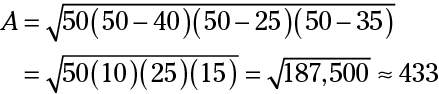
You've marked off an area of approximately 433 square yards.





