Population dynamics are changes in population density over time or in a particular area. Primarily, populations increase because of births (natality) and decrease because of deaths (mortality).
The rate at which a population increases (r) depends on the relative number of births (B) and deaths (D) during a particular time interval:
r = B – D
To figure out how many individuals are added to or subtracted from a population (in other words, how much a population grows or decreases), you also have to take into account the size of the population itself. The rate of growth (G) of a population is equal to its rate of increase (r) times the population size (N):
G = r x N
If a population has unlimited resources like food, water, and space, it has the potential to keep increasing at a steady rate, resulting in exponential growth like that shown in part a of this figure.
The maximum growth rate of a population under ideal conditions is referred to as biotic potential.
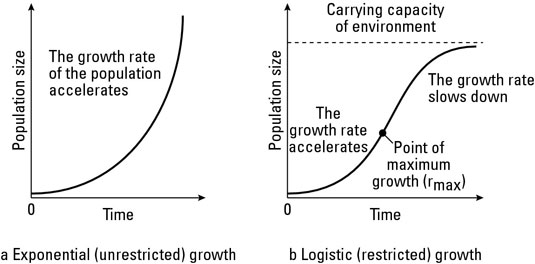
In nature, resources are usually limited, and population growth can be limited by a number of environmental factors, which population ecologists group into two categories:
Density-dependent factors are more likely to limit growth as population density increases.
Density-independent factors limit growth but aren’t affected by population density.
Thus, most natural populations exhibit logistic growth, where the growth rate decreases as the population size increases, like that shown in part b.
Ecologists call the maximum population a particular habitat can sustain its carrying capacity. As populations approach the carrying capacity, density-dependent factors have a greater effect, and population growth slows dramatically.
Scientists have followed groups of organisms all born at the same time and looked at their survivorship — the number of organisms in the group that were still alive at different times after birth. They noticed that three different patterns appeared when they plotted out survivorship curves — graphs that plot survival over time after birth, like the ones in this figure:
Type I survivorship: Most offspring survive, and organisms live out most of their life span, dying in old age.
Type II survivorship: Death occurs randomly throughout the life span, usually due to predation or disease.
Type III survivorship: Most organisms die young, and few members of the population survive to reproductive age. However, individuals that do survive to reproductive age often live out the rest of their life span and die in old age.

Test your understanding of population dynamics with the following questions.
You put 10,000 bacterial cells in a test tube containing fresh food. These bacteria reproduce once per hour, and no significant amount of deaths occur for 12 hours. How many bacteria are in the population after just 1 hour?
A population of fruit flies is growing exponentially on some spoiled fruit. The intrinsic rate of increase for the population is 6 percent per day. If you start out with 10 fruit flies, how many fruit flies will you have in two days?
For questions 3–6, use the following terms to identify which factors affect the populations in each question.
Density-dependent
Density-independent
The availability of light in a forest limits the growth of plants.
A hurricane destroys a swamp ecosystem.
Birds compete for nesting sites in a forest.
A viral infection kills bees.
For questions 7–10, use the following terms to identify which type of survivorship the population in each question exhibits.
Type I
Type II
Type III
Sea turtles bury their eggs in the sand and leave them. As the baby turtles hatch and make their way to the ocean, sea birds prey upon them. Very few baby turtles make it to the ocean.
Elephants have few offspring, but they invest a lot of care in the offspring that they have, helping to ensure that the offspring survive to adulthood.
A maple tree produces hundreds of seeds that fly off in the air. Many seeds germinate, but few grow to be adult trees.
Sea jellies (jellyfish) hatch from eggs, grow into small planktonic jellies, and then keep growing until they reach their adult size. Throughout their lives they may die because of predation or natural occurrences like storms.
The following are the answers to the practice questions.
The starting population size (N) = 10,000. The rate of growth (r) is 100 percent every hour. You can represent 100 percent as the proportion 1.0. So G = 1.0 x 10,000 = 10,000. After an hour, the total number in the population equals the original population plus the growth: N = 10,000 + 10,000 = 20,000.
The answer is 11 fruit flies.
G = rN; r = 6 percent, which is 0.06 of the population per day for two days. The population starts out as 10 fruit flies. Growth of the population after one day is G = 0.06 x 10 = 0.6, making the total population N = 10 + 0.6 = 10.6. Growth on day two is G = 0.06 x 10.6 = 0.636; N = 10.6 + 0.636 = 11.236.
The answer is 1. Density-dependent.
As plants in a forest grow, they begin to shade each other, cutting down on the availability of light and limiting the growth of some plants.
The answer is 2. Density-independent.
The answer is 1. Density-dependent.
The answer is 1. Density-dependent.
Viral disease is density-dependent because viruses are transmitted from one bee to another. Organisms that live in dense populations have a greater chance of being exposed to an infectious disease.
The answer is 3. Type III.
The answer is 1. Type I.
The answer is 3. Type III.
The answer is 2. Type II.






