You can convert from the magnitude/angle way of specifying a vector to the coordinate way of expression. Doing so is essential for the kinds of operations you can expect to execute on vectors, such as when adding vectors.
For example, you have one vector at 15 degrees and one at 19 degrees, and you want to add them together. How the heck do you do that? If you were to convert them into their coordinates, (a, b) and (c, d), the answer would be trivial because you only have to add the x and y coordinates to get the answer: (a + c, b + d).
To see how to convert between the two ways of looking at vectors, take a look at vector v in the figure. The vector can be described as having a magnitude v at an angle of theta.
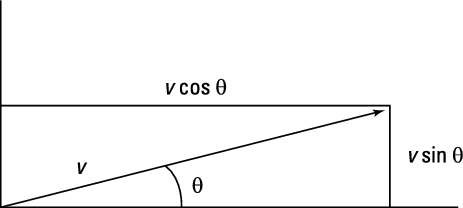
To convert this vector into the coordinate way of looking at vectors, you have to use the trigonometry shown in the figure. The x coordinate equals v cos theta, and the y coordinate equals v sin theta:
vx = v cos theta
vy = v sin theta
Keep these relationships in mind because you’ll come across them often in physics questions.
Sample question
Suppose that you’ve walked away from the origin so you’re now 5.0 kilometers from the origin, at an angle of 45 degrees. Resolve that into vector coordinates.
The correct answer is (3.5, 3.5) km.
Apply the equation vx = v cos theta to find the x coordinate. That’s 5.0 cos 45 degrees, or 3.5.
Apply the equation vy = v sin theta to find the y coordinate. That’s 5.0 sin 45 degrees, or 3.5.
Practice questions
Resolve a vector 3.0 meters long at 15 degrees into its components.
Resolve a vector 9.0 meters long at 35 degrees into its components.
Resolve a vector 6.0 meters long at 125 degrees into its components.
Resolve a vector 4.0 meters long at 255 degrees into its components.
Following are answers to the practice questions:
(2.9, 0.8) m
Apply the equation vx = v cos theta to find the x coordinate: 3.0 x cos 15 degrees, or 2.9.
Apply the equation vy = v sin heta to find the y coordinate: 3.0 x sin 15 degrees, or 0.8.
(7.4, 5.2) m
Apply the equation vx = v cos theta to find the x coordinate: 9.0 x cos 35 degrees, or 7.4.
Apply the equation vy = v sin theta to find the y coordinate: 9.0 x sin 35 degrees, or 5.2.
(–3.4, 4.9) m
Apply the equation vx = v cos theta to find the x coordinate: 6.0x cos 125 degrees, or –3.4.
Apply the equation vy = v sin theta to find the y coordinate: 6.0 x sin 125 degrees, or 4.9.
(–1.0, –3.9) m
Apply the equation vx = v cos theta to find the x coordinate: 4.0 x cos 255 degrees, or –1.0.
Apply the equation vy = v sin theta to find the y coordinate: 4.0 x sin 255 degrees, or –3.9.






