How to Measure Linear Expansion in a Solid Due to Temperature Increase

When you talk about the expansion of a solid in any one dimension under the influence of heat, you’re talking about linear expansion. Thanks to physics, you can measure how much a solid will expand based on how much its temperature changes.

The figure shows an image of this phenomenon.

Linear expansion usually takes place when you apply heat to solids.

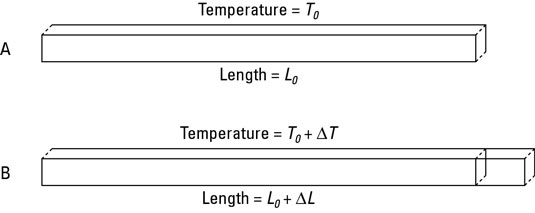
Under thermal expansion, a solid object’s change in length,

is proportional to the change in temperature,

You can show this relationship mathematically.

Note: This example uses a subscript 0 (L₀, for example), which is common in texts for these kinds of equations.

First, suppose you raise the temperature of an object a small amount:

The change of temperature results in an expansion in any linear dimension of

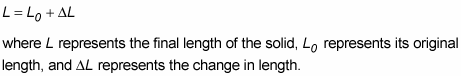
When you heat a solid, the solid expands by a few percent, and that percentage is proportional to the change in temperature. In other words,

is proportional to

The constant of proportionality, which helps tell you exactly how much an object will expand, depends on which material you’re working with. The constant of proportionality is the coefficient of linear expansion, which you give the symbol

You can write this relationship as an equation this way:

However, because the units of Celsius and Kelvin are the same size, a difference in temperature measured in degrees Celsius is of the same magnitude when measured in kelvin. Therefore, to convert the coefficient of linear expansion from degrees Celsius to kelvin, you only have to swap the symbols.

Plenty of construction projects take linear expansion into account. You often see bridges with “expansion joints” connecting the bridge to the road surface. As temperatures rise, these joints allow the bridge materials to expand without buckling.

Here’s a construction-based example. Say that you’re called in to check out a new railroad. You look closely at the 10.0-meter-long rails, noticing that they’re only 1.0 millimeter apart at the ends. “How much hotter does it get around these parts during the summer?” you ask.

“Hotter?” the chief designer guffaws. “You afraid the rails will melt?”

Everyone snickers at your ignorance as you check your almanac, which tells you that you can expect the rails to get 50 degrees Celsius hotter during a normal summer. The coefficient of linear expansion for the steel that the rails are made from is approximately

So how much will the typical rail expand during the hot part of summer? You know that

Plugging in the numbers gives you the expansion:

In other words, you can expect the rails to expand

or 6.0 millimeters, in the summer. However, the rails are only 1.0 millimeter apart. The railroad company is in trouble.

You look at the chief designer and say, “You and I are about to have a nice, long talk about physics.”