Albert Einstein was influenced by the concept of an unchanging universe. His general theory of relativity predicted a dynamic universe — one that changed substantially over time — so he introduced a term, called the cosmological constant, into the theory to make the universe static and eternal. This term represented a form of repulsive gravity that exactly balanced out the attractive pull of gravity, and it would prove to be a mistake when, several years later, astronomer Edwin Hubble discovered that the universe was expanding. Even today, the consequence of the cosmological constant in general relativity has enormous impact upon physics, causing string theorists to rethink their whole approach.
Discovering that energy and pressure have gravity
In Newton’s gravity, bodies with mass were attracted to each other. Einstein’s relativity showed that mass and energy were related. Therefore, mass and energy both exerted gravitational influence. Not only that, but it was possible that space itself could exert a pressure that warped space. Several models were constructed to show how this energy and pressure affected the expansion and contraction of space.
When Einstein created his first model based on the general theory of relativity, he realized that it implied an expanding universe. At the time, no one had any particular reason to think the universe was expanding, and Einstein assumed that this was a flaw in his theory.
Einstein’s general relativity equations allowed for the addition of an extra term while remaining mathematically viable. Einstein found that this term could represent a positive energy (or negative pressure) uniformly distributed throughout the fabric of space-time itself, which would act as an antigravity, or repulsive form of gravity. This term was chosen to precisely cancel out the contraction of the universe, so the universe would be static (or unchanging in time).
In 1917, the same year Einstein published his equations containing the cosmological constant, Dutch physicist Willem de Sitter applied them to a universe without matter, in which the only thing that exists is the energy of the vacuum — the cosmological constant itself. Even in a universe containing no matter at all, this means that space will expand.
A de Sitter space has a positive value for the cosmological constant, which can also be described as a positive curvature of space-time. A similar model with a negative cosmological constant (or a negative curvature, in which expansion is slowing) is called an anti-de Sitter space.
In 1922, the Russian physicist Aleksandr Friedmann turned his hand to solving the elaborate equations of general relativity, but decided to do so in the most general case by applying the cosmological principle (which can be seen as a more general case of the Copernican principle), which consists of two assumptions:
The universe looks the same in all directions (it’s isotropic).
The universe is uniform no matter where you go (it’s homogenous).
With these assumptions, the equations become much simpler. Einstein’s original model and de Sitter’s model both ended up being special cases of this more general analysis. Friedmann was able to define the solution depending on just three parameters:
Hubble’s constant (the rate of expansion of the universe)
Lambda (the cosmological constant)
Omega (average matter density in the universe)
To this day, scientists are trying to determine these values as precisely as they can, but even without real values they can define three possible solutions. Each solution matches a certain “geometry” of space, which can be represented in a simplified way by the way space naturally curves in the universe, as shown in Figure 9-2.
Closed universe: There is enough matter in the universe that gravity will eventually overcome the expansion of space. The geometry of such a universe is a positive curvature, such as the sphere in the leftmost image in the figure below. (This matched Einstein’s original model without a cosmological constant.)
Open universe: There isn’t enough matter to stop expansion, so the universe will continue to expand forever at the same rate. This space-time has a negative curvature, like the saddle shape shown in the middle image in the figure below.
Flat universe: The expansion of the universe and the density of matter perfectly balance out, so the universe’s expansion slows down over time but never quite stops completely. This space has no overall curvature, as shown in the rightmost image of the figure below. (Friedmann himself didn’t discover this solution; it was found years later.)
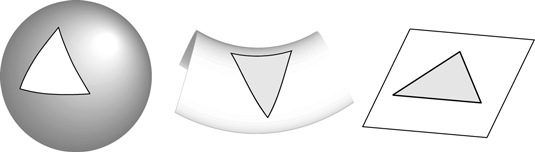 Three types of universes: closed, open, and flat.
Three types of universes: closed, open, and flat.
These models are highly simplified, but they needed to be because Einstein’s equations got very complex in cases where the universe was populated with a lot of matter, and supercomputers didn’t yet exist to perform all the math (and even physicists want to go on dates every once in a while).
Hubble proves an expanding universe
In 1927, astronomer Edwin Hubble proved that the universe is expanding. While studying distant galaxies, he noticed that the light from their stars had a wavelength that was shifted toward the red end of the electromagnetic spectrum. This is a consequence of the wave nature of light — an object that’s moving (with respect to the observer) emits light with a slightly different wavelength. (If you’ve ever heard a siren’s pitch change as it approaches and passes you, you’ve experienced this effect.)
Hubble saw this redshift in the stars he observed, caused not only by the motion of the stars but by the expansion of space-time itself, and in 1929 determined that the amount of shift was related to the distance from Earth. The more distant stars were moving away faster than the nearby stars. Space itself was expanding.
Clearly, in this case, Einstein had been wrong and Friedmann had been right to explore all the possible scenarios predicted by general relativity. Einstein called the introduction of the cosmological constant his “biggest blunder” and removed it from the equations. Unfortunately, Friedmann died in 1925, so he never knew he was right.






