In trying to understand the universe, two major problems remained: the flatness problem and the horizon problem. To solve these, the big bang theory is modified by the inflation theory, which states that the universe expanded rapidly shortly after it was created. Today, the principles at the heart of inflation theory have a profound impact on the way that string theory is viewed by many physicists.
These two problems can be stated simply as:
-
Horizon problem: The CMBR is essentially the same temperature in all directions.
-
Flatness problem: The universe appears to have a flat geometry.
The universe's issues: Too far and too flat
The horizon problem (also sometimes called the homogeneity problem) is that no matter which direction you look in the universe, you see basically the same thing (see the following figure). The cosmic microwave background radiation (CMBR) temperatures throughout the universe are, to a very high level of measurement, almost exactly the same temperature in every direction. This really shouldn't be the case, if you think about it more carefully.

If you look in one direction in space, you're actually looking back in time. The light that hits your eye (or telescope) travels at the speed of light, so it was emitted years ago. This means there's a boundary of 14 billion (or so) light-years in all directions. (The boundary is actually farther because space itself is expanding, but you can ignore that for the purposes of this example.) If there is anything farther away than that, there is no way for it to have ever communicated with us. So you look out with your powerful telescope and can see the CMBR from 14 billion light-years away (call this Point A).
If you now look 14 billion light-years in the opposite direction (call this Point B), you see exactly the same sort of CMBR in that direction. Normally, you'd take this to mean that all the CMBR in the universe has somehow diffused throughout the universe, like heating up an oven. Somehow, the thermal information is communicated between Points A and B.
But Points A and B are 28 billion light-years apart, which means, because no signal can go faster than the speed of light, there's no way they could have communicated with each other in the entire age of the universe. How did they become the same temperature if there's no way for heat to transfer between them? This is the horizon problem.
The flatness problem has to do with the geometry of our universe, which appears (especially with recent WMAP evidence) to be a flat geometry, as pictured in the following figure. The matter density and expansion rate of the universe appear to be nearly perfectly balanced, even 14 billion years later when minor variations should have grown drastically. Because this hasn't happened, physicists need an explanation for why the minor variations haven't increased dramatically. Did the variations not exist? Did they not grow into large-scale variations? Did something happen to smooth them out? The flatness problem seeks a reason why the universe has such a seemingly perfectly flat geometry.
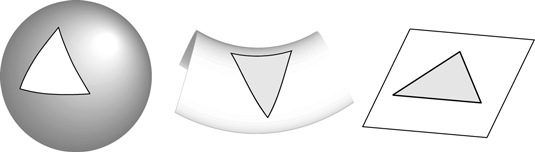
These three types of universes are simplified representations of the way space naturally curves in the universe:
-
Closed universe: There is enough matter in the universe that gravity will eventually overcome the expansion of space. The geometry of such a universe is a positive curvature. (This matched Einstein's original model without a cosmological constant.)
-
Open universe: There isn't enough matter to stop expansion, so the universe will continue to expand forever at the same rate. This space-time has a negative curvature (saddle-shaped).
-
Flat universe: The expansion of the universe and the density of matter perfectly balance out, so the universe's expansion slows down over time but never quite stops completely. This space has no overall curvature.
Rapid expansion early on holds the solutions
In 1980, astrophysicist Alan Guth proposed the inflation theory to solve the horizon and flatness problems (although later refinements by Andrei Linde, Andreas Albrecht, Paul Steinhardt, and others were required to get it to work). In this model, the early universal expansion accelerated at a rate much faster than we see today.
It turns out that the inflationary theory solves both the flatness problem and horizon problem (at least to the satisfaction of most cosmologists and astrophysicists). The horizon problem is solved because the different regions we see used to be close enough to communicate, but during inflation, space expanded so rapidly that these close regions were spread out to cover all of the visible universe.
The flatness problem is resolved because the act of inflation actually flattens the universe. Picture an uninflated balloon, which can have all kinds of wrinkles and other abnormalities. As the balloon expands, though, the surface smoothes out. According to inflation theory, this happens to the fabric of the universe as well.
In addition to solving the horizon and flatness problems, inflation also provides the seeds for the structure that we see in our universe today. Tiny energy variations during inflation, due simply to quantum uncertainty, become the sources for matter to clump together, eventually becoming galaxies and clusters of galaxies.
One issue with the inflationary theory is that the exact mechanism that would cause — and then turn off — the inflationary period isn't known. Many technical aspects of inflationary theory remain unanswered, though the models include a scalar field called an inflaton field and a corresponding theoretical particle called an inflaton. Most cosmologists today believe that some form of inflation likely took place in the early universe.






