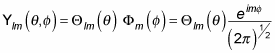At some point, your quantum physics instructor may ask you to find the eigenfunctions of Lz in spherical coordinates. In spherical coordinates, the Lz operator looks like this:
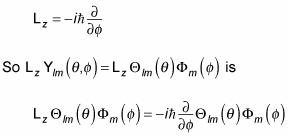
which is the following:
And because
this equation can be written in this version:
Cancelling out terms from the two sides of this equation gives you this differential equation:
This looks easy to solve, and the solution is just
where C is a constant of integration.
You can determine C by insisting that
be normalized — that is, that the following hold true:
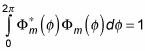
(Remember that the asterisk symbol [*] means the complex conjugate. A complex conjugate flips the sign connecting the real and imaginary parts of a complex number.)
So this gives you
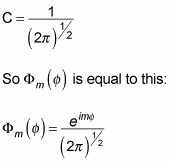
You are now able to determine the form of
which equals