In quantum physics, you can use the Schrödinger equation to see how the wave function for a particle in an infinite square well evolves with time. The Schrödinger equation looks like this:
You can also write the Schrödinger equation this way, where H is the Hermitian Hamiltonian operator:
That’s actually the time-independent Schrödinger equation. The time-dependent Schrödinger equation looks like this:
Combining the preceding three equations gives you the following, which is another form of the time-dependent Schrödinger equation:
And because you’re dealing with only one dimension, x, this equation becomes
This is simpler than it looks, however, because the potential doesn’t change with time. In fact, because E is constant, you can rewrite the equation as
That equation makes life a lot simpler — it’s easy to solve the time-dependent Schrödinger equation if you’re dealing with a constant potential. In this case, the solution is
Neat. When the potential doesn’t vary with time, the solution to the time-dependent Schrödinger equation simply becomes
the spatial part, multiplied by
the time-dependent part.
So when you add in the time-dependent part to the time-independent wave function, you get the time-dependent wave function, which looks like this:
The energy of the nth quantum state is
Therefore, the result is
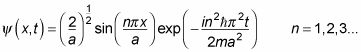
where exp (x) = ex.






