Finding the Total Energy Equation for Three-Dimensional Free Particle Problems

At some point, your quantum physics instructor may want you to find the total energy equation for three-dimensional free particle problems. The total energy of the free particle is the sum of the energy in three dimensions:

E = E_x + E_y + E_z

With a free particle, the energy of the x component of the wave function is

And this equation works the same way for the y and z components, so here’s the total energy of the particle:

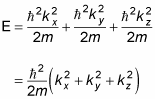
Note that k_x² + k_y² + k_z² is the square of the magnitude of k — that is,

Therefore, you can write the equation for the total energy as

Note that because E is a constant, no matter where the particle is pointed, all the eigenfunctions of

are infinitely degenerate as you vary k_x, k_y, and k_z.