How to Determine the Allowed Energies of a Hydrogen Atom

When you apply the quantum mechanical Schrödinger equation for a hydrogen atom, the quantization condition for the wave function of r to remain finite as r goes to infinity is

where

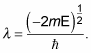
Substituting

into the quantization-condition equation gives you the following:

Now solve for the energy, E. Squaring both sides of the preceding equation gives you

So here’s the energy, E (Note: Because E depends on the principal quantum number, you rename it E_n):

Physicists often write this result in terms of the Bohr radius — the orbital radius that Niels Bohr calculated for the electron in a hydrogen atom, r₀. The Bohr radius is

And in terms of r₀, here’s what E_n equals:

The ground state, where n = 1, works out to be about E = –13.6 eV.

Notice that this energy is negative because the electron is in a bound state — you’d have to add energy to the electron to free it from the hydrogen atom. Here are the first and second excited states:

• First excited state, n = 2: E = –3.4 eV

• Second excited state, n = 3: E = –1.5 eV

So you’ve now used the quantization condition, which is

to determine the energy levels of the hydrogen atom.