How to Find the Energy of a Charged Oscillator Using the Perturbation Theory

In quantum physics, when you have the exact eigenvalues for a charged oscillator in a perturbed system, you can find the energy of the system. Based on the perturbation theory, the corrected energy of the oscillator is given by

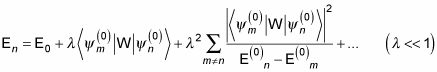
where

is the perturbation term in the Hamiltonian. That is, here,

Now take a look at the corrected energy equation using

The first-order correction is

which, using

becomes

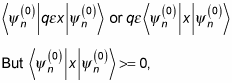
because that's the expectation value of x, and harmonic oscillators spend as much time in negative x territory as in positive x territory — that is, the average value of x is zero. So the first-order correction to the energy, as given by perturbation theory, is zero.

Okay, what's the second-order correction to the energy, as given by perturbation theory? Here it is:

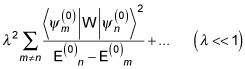
And because

you have

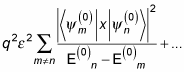
Cast this in terms of bras and kets, changing

making the second-order energy correction into this expression:

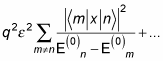
You can decipher this step by step. First, the energy is

That makes figuring out the second-order energy a little easier.

Also, the following expressions turn out to hold for a harmonic oscillator:

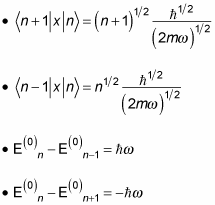
With these four equations, you're ready to tackle

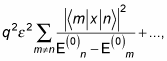
the second-order correction to the energy. Omitting higher-power terms, the summation in this equation becomes

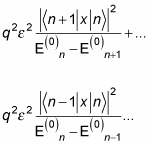
And substituting in for E⁽⁰⁾_n – E⁽⁰⁾_{n + 1} and E⁽⁰⁾_n – E⁽⁰⁾_{n– 1} gives you

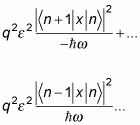
Now, substituting in for n + 1 | x | n > and n – 1 | x | n > gives you

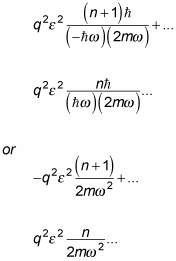
So the second-order correction is

Therefore, according to perturbation theory, the energy of the harmonic oscillator in the electric field should be

Compare this result to the earlier equation for the exact energy levels,

In other words, perturbation theory has given you the same result as the exact answer. How's that for agreement?

Of course, you can't expect to hit the same answer every time using perturbation theory, but this result is impressive!