In quantum physics, if you are given the wave equation for a particle in an infinite square well, you may be asked to normalize the wave function. For example, start with the following wave equation:
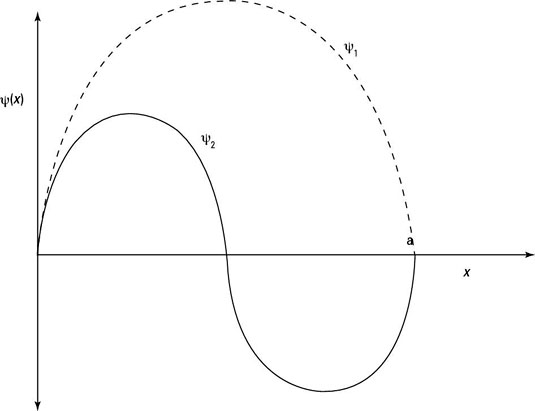
The wave function is a sine wave, going to zero at x = 0 and x = a. You can see the first two wave functions plotted in the following figure.
Normalizing the wave function lets you solve for the unknown constant A. In a normalized function, the probability of finding the particle between
adds up to 1 when you integrate over the whole square well, x = 0 to x = a:
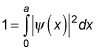
Substituting for
gives you the following:
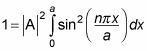
Here’s what the integral in this equation equals:
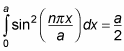
So from the previous equation,
Solve for A:
Therefore, here’s the normalized wave equation with the value of A plugged in:
And that’s the normalized wave function for a particle in an infinite square well.






