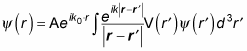How to Relate the Scattering Amplitude and Differential Cross Section of Spinless Particles

The scattering amplitude of spinless particles is crucial to understanding scattering from the quantum physics point of view. To see that, take a look at the current densities, J_inc (the flux density of a given incident particle) and J_sc (the current density for a given scattered particle):

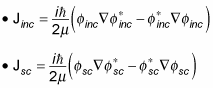
(Remember that the asterisk symbol [*] means the complex conjugate. A complex conjugate flips the sign connecting the real and imaginary parts of a complex number.)

Inserting your expressions for

into these equations gives you the following, where

is the scattering amplitude:

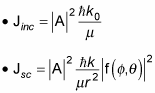
Now in terms of the current density, the number of particles

scattered into

and passing through an area

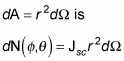
Plugging in

into the preceding equation gives you

Also, recall that

You get

And here's the trick — for elastic scattering, k = k₀, which means that this is your final result:

The problem of determining the differential cross section breaks down to determining the scattering amplitude.

To find the scattering amplitude — and therefore the differential cross section — of spinless particles, you work on solving the Schrödinger equation:

You can also write this as

You can express the solution to that differential equation as the sum of a homogeneous solution and a particular solution:

The homogeneous solution satisfies this equation:

And the homogeneous solution is a plane wave — that is, it corresponds to the incident plane wave:

To take a look at the scattering that happens, you have to find the particular solution. You can do that in terms of Green's functions, so the solution to

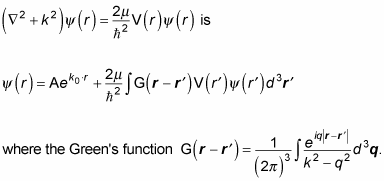
This integral breaks down to

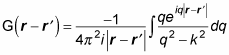
You can solve the preceding equation in terms of incoming and/or outgoing waves. Because the scattered particle is an outgoing wave, the Green's function takes this form:

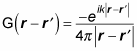
You already know that

So substituting

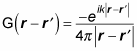
into the preceding equation gives you