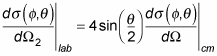In quantum physics, once you relate the angles of the scattered particles in the lab frame and the center-of-mass frame, you can translate the differential cross section — the bull's eye when you're aiming to scatter the particles at a particular angle — between the lab and center-of-mass frames.
The differential area
is infinitesimal in size, and it stays the same between the two frames. But the angles that make up
the scattering angle, vary when you translate between frames. You get to take a look at how that works now, relating the lab differential cross section:
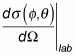
to the center-of-mass differential cross section:
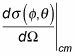
In the lab frame,
And in the center-of-mass frame,
Because
the following equation is true:
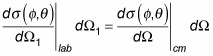
Putting that equation with the equations for the lab frame and the center-of-mass frame, you have
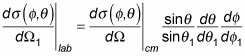
Because you have cylindrical symmetry here,
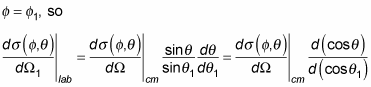
You've already seen that
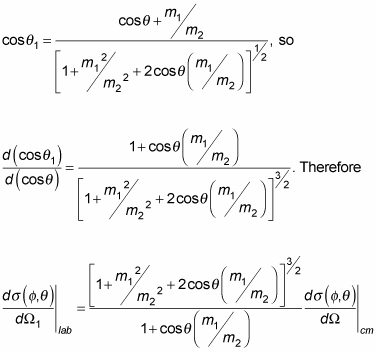
You can also show that