Spin One-Half Matrices

In quantum physics, when you look at the spin eigenstates and operators for particles of spin 1/2 in terms of matrices, there are only two possible states, spin up and spin down.

The eigenvalues of the S² operator are

and the eigenvalues of the S_z operator are

You can represent these two equations graphically as shown in the following figure, where the two spin states have different projections along the z axis.

Spin magnitude and z projection.

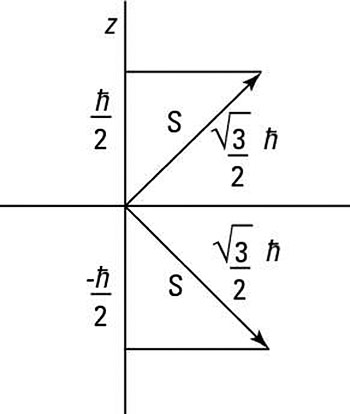
In the case of spin 1/2 matrices, you first represent the eigenstate

like this:

And the eigenstate

looks like this:

Now what about spin operators like S²? The S² operator looks like this in matrix terms:

And this works out to be the following:

Similarly, you can represent the S_z operator this way:

This works out to

Using the matrix version of S_z, for example, you can find the z component of the spin of, say, the eigenstate

Finding the z component looks like this:

Putting this in matrix terms gives you this matrix product:

Here’s what you get by performing the matrix multiplication:

And putting this back into ket notation, you get the following:

How about the raising and lowering operators S₊ and S_–? The S₊ operator looks like this:

And the lowering operator looks like this:

Here it is in matrix terms:

Performing the multiplication gives you this:

Or in ket form, it’s

Cool.