For the ACT Math test, you definitely want to know how to work with matrices. Fortunately, adding and subtracting matrices are both simple and similar operations.
A matrix is a grid of numbers or variables arranged in horizontal rows and vertical columns.
The figure shows a variety of matrices.
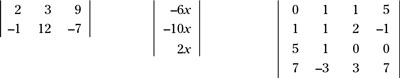
The dimensions of the matrices (that is, the number of rows and columns) in the figure are
respectively. By convention, the number of rows is stated first and the number of columns second.
Adding matrices is easy: Just add pairs of corresponding numbers in the matrix and place the results in a new matrix.
The two matrices you’re adding must have identical horizontal and vertical dimensions. As a result, the new matrix always has the same dimensions as the two matrices you’re adding.
Example 1
Which of the following is the result when you add
and

To find the correct answer, simply add each pair of corresponding numbers
and then place them in the same positions in a new matrix. The correct answer is Choice (C).
Subtracting matrices is similar to adding them: For each pair of corresponding numbers in the matrix, subtract the second number from the first and then place the results in a new matrix. As with addition, you can only subtract one matrix from another if both matrices have identical horizontal and vertical dimensions.
Example 2
Which of the following is the result when you perform this matrix subtraction:
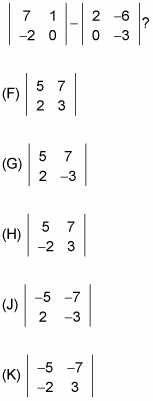
Subtract each pair of corresponding numbers in order
and then place them in the same positions in a new matrix. The correct answer is Choice (H).






