The first type of problem on the Assembling Objects subtest of the ASVAB presents you with simple geometric figures such as stars, cloud shapes, letter shapes, circles, and triangles. In the first drawing, you can see shapes and lines labeled with dots and the letters A and B. These letters and dots indicate points of attachment.
The next four drawings show possible solutions of what the shapes would look like if connected at designated points by the line. The shapes may be reoriented or rotated from what you observe in the first drawing. The correct solution shows the line connected correctly to reflect the points shown in the first drawing.
Look at this drawing and see whether you can solve it. In the first drawing, you see a star and a sort of lopsided T. There’s a small dot on the short appendage of the T, labeled A, and a dot on one of the points of the star, labeled B.
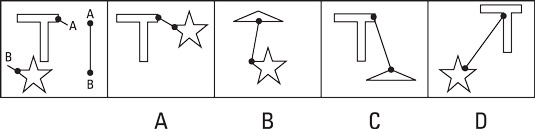
Choice (A) is the correct solution. Choices (B) and (C) include shapes that aren’t included in the first drawing, so they’re obviously incorrect. Although Choice (D) has the correct shapes, they aren’t connected at the same points depicted in the first drawing.
Okay that sounds simple, doesn’t it? Don’t worry; it gets more complicated (sorry to burst your bubble). The example below shows the same problem but with a different twist.
Choice (A) is the correct solution for this problem. In this case, the two shapes have been repositioned and rotated.
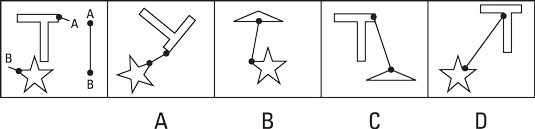
On the flip side: Avoiding mirrors
Mirroring (or flipping or reflecting) isn’t the same as rotation. The shape in Box B isn’t the same as the shape in Box A. It’s a mirror image. No matter how you rotate the shape in Box A, it will never look like the shape in Box B. Think of it this way: You can turn a jigsaw puzzle piece upside down (so the picture side is facing the table), and it may fit, but that’s not the proper method of putting the puzzle together. (It wouldn’t look very pretty, either.)
The Assembling Objects subtest is the same way. The possible solutions may include shapes that are reflections of a shape shown in the first drawing, but they’ll never be the correct solution.
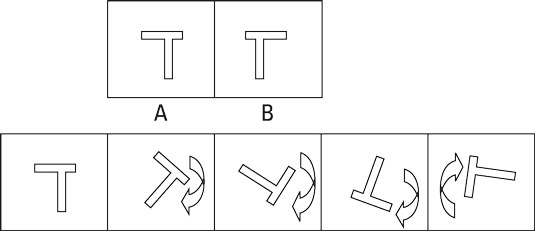
Crossing over the right places
If a shape in the first drawing shows a line that goes through any part of the shape, the correct solution must also reflect the same line-shape relationship. Check out the example below. In the first drawing, Point B is in the center of the star. But note the line intersects the star at one of its indentations and not one of its points. That means the correct solution must show the same intersection.
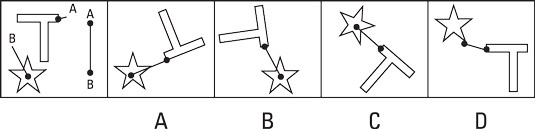
In this example, Choice (B) is the correct solution. At first glance, Choice (C) looks like it could be correct. Can you spot the reason it’s not the correct solution? Right! The lopsided T shape in the image is a reflection of the shape shown in the first drawing.
Putting it all together
You’re starting to see the shape of things! (These little zingers just keep popping out.) Try a couple more, just to get into shape.
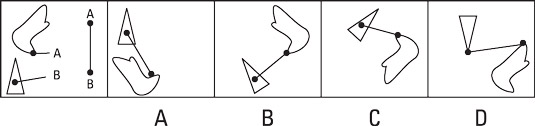
In this example, did you select Choice (C) as the correct answer? If so, good job! Choice (A) is incorrect because the line intersects the triangle at the wrong point and the connection point A is misplaced. Choice (B) is incorrect because the weird shape is actually a mirror image of the shape shown in the first drawing. Choice (D) is incorrect because the points don’t correlate to the points depicted in the first drawing.
Now try the following example. The first drawing includes a shape that kind of looks like a Y and a shape that looks like the letter C.
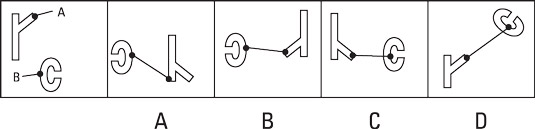
The correct answer is Choice (B). Choice (A) is incorrect because the Y shape is a mirror image of the shape shown in the first drawing, and the connection points don’t correspond to the first drawing’s points. Choice (C) is incorrect because the Y shape is a mirror image of the shape shown in the first drawing.
Choice (D) is incorrect because the Y shape is a different shape (the stem is much shorter) than the shape shown in the first drawing and because the connection dot on the C shape is in the wrong location.






