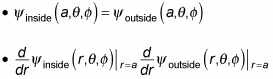In quantum physics, you can apply the radial equation outside a square well (where the radius is greater than a). In the region r > a, the particle is just like a free particle, so here's what the radial equation looks like:
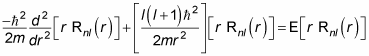
You solve this equation as follows:
you substitute
so that Rnl(r) becomes
Using this substitution means that the radial equation takes the following form:
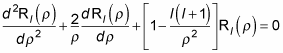
The solution is a combination of spherical Bessel functions and spherical Neumann functions, where Bl is a constant:
If the energy E l = i Bl", so that the wave function decays exponentially at large distances r. So the radial solution outside the square well looks like this, where
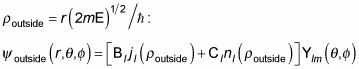
Given that the wave function inside the square well is
So how do you find the constants Al and Bl? You find those constants through continuity constraints: At the inside/outside boundary, where r = a, the wave function and its first derivative must be continuous. So to determine Al and Bl, you have to solve these two equations: