Variable costs change in response to certain stimuli, called cost drivers. Get it? Cost drivers drive up the cost. For example, a common cost driver is the number of units produced. Units produced is the cost driver for total direct materials; the more units that you produce, the more direct materials you need.
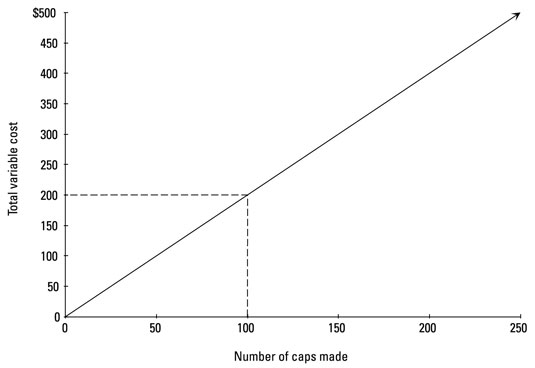
Suppose that your factory manufactures baseball caps and that every baseball cap requires two square feet of fabric, which costs $1 per square foot. Manufacturing 100 baseball caps requires 200 square feet of fabric (100 caps x 2 square feet per hat). Therefore, you can determine that this batch of hats costs $200 (200 square feet x $1).
You can graphically represent costs by charting total cost (on the left axis) against the cost driver (on the bottom axis). You can see how producing 100 caps drives total variable costs of $200.
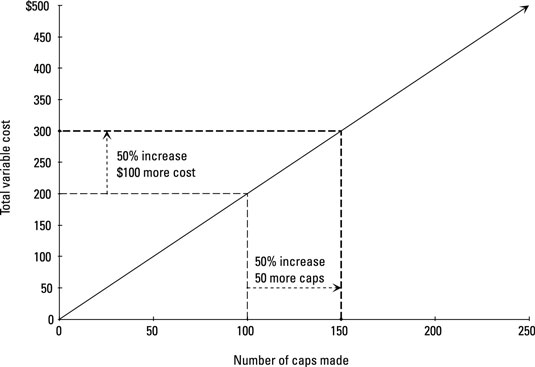
A change in a cost driver always results in a corresponding change to the total cost. For example, increasing the cost driver by 50 percent causes total variable costs to increase by 50 percent.
When it comes to manufacturing your caps, then, increasing the number of caps produced by 50 percent (to 150; $100 + [0.5 x $100]) costs 50 percent more, or $300 ($200 + [0.5 x $200]).
A 50 percent increase in the number of caps made affects total variable costs. Producing 50 more units (a 50-percent bump) increases total variable costs by $100 (a 50-percent rise in total variable costs).
Most direct costs are variable with respect to the number of units produced. Direct labor (the cost of employee wages that can be directly traced to the products those employees make) is another common variable cost. Take a shoe factory as an example: The more shoes the factory makes, the higher the direct labor cost.
Variable cost per unit describes the relationship between the cost driver (say, the number of units produced) and total cost (direct materials or direct labor). Just multiply the variable cost per unit by the cost driver to get total cost. Suppose a shoe factory’s variable cost per unit of direct labor is $30. To make 1,000 shoes, the factory must pay a total of $30,000 for direct labor.
To compute variable cost per unit, divide total variable cost by the number of units produced.
Variable cost per unit usually does not change with volume. To graph the relationship between the cost driver and variable cost per unit, draw a horizontal line as shown. Here, the variable cost per unit of direct materials needed to make baseball caps is $2 per unit. Even when the company ratchets up production from 100 caps to 150, the variable cost per unit remains steady at $2.
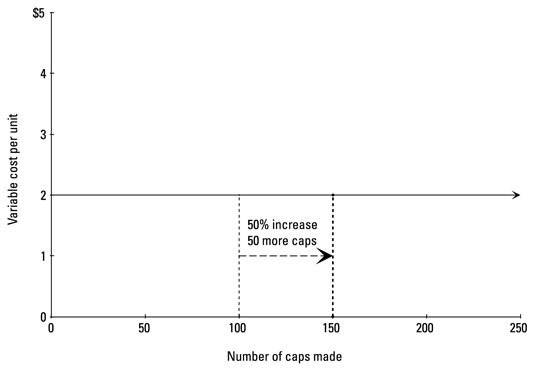
As the activity level changes, don’t confuse total variable costs with variable costs per unit. Total variable costs change in proportion to the change in activity level (diagonal line pointing upward), while variable costs per unit remain the same (horizontal line).






