Here is a brief refresher for some of the important rules of calculus differentiation for managerial economics. While calculus is not necessary, it does make things easier.
Constant function rule
If variable y is equal to some constant a, its derivative with respect to x is 0, or if
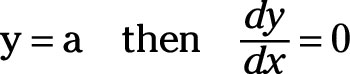
For example,

Power function rule
A power function indicates that the variable x is raised to a constant power k.
The derivative of y with respect to x equals k multiplied by x raised to the k-1 power, or

For example,
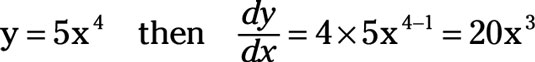
The power function rule is extremely powerful! You can use it with a variety of exponents. For example,
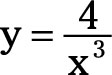
can be rewritten as
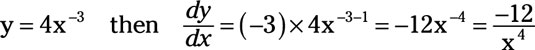
Be careful with this last derivative. When a variable with an exponent appears in the denominator, such as x3 in the previous equation, the variable can be moved to the numerator, but the exponent becomes negative. So, 4/x3 becomes 4x-3. Then when you take the derivative, make sure you subtract 1 from –3 to get –4.
As another example, consider
can be written as
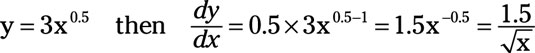
You may remember that square roots are fractional exponents, or the 0.5 (one-half) power.
Finally, note that
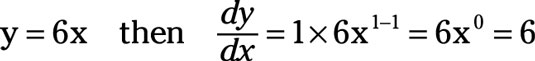
Sum-difference rule
Assume there are two functions, TR = g(q) and TC = h(q).
You may think of the variable TR as total revenue, the variable TC as total cost, and the variable q as the quantity of the product produced. The symbol g in the total revenue function and the symbol h in the total cost function mean that the relationship between q and total revenue is different from the relationship between q and total cost.
Further, assume that the variable ð (profit) is a function of both TR and TC, so
ð = <i>TR</i> – <i>TC</i>.
The derivative of ð with respect to q equals the sum (the functions can be added or subtracted) of the derivatives of TR and TC with respect to q, or,
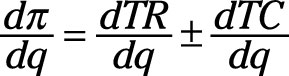
For example,
Then the derivatives of TR and TC with respect to q are
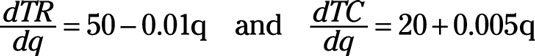
Using the sum-difference rule
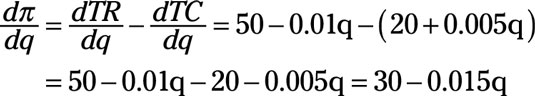
Although in the example the two functions were subtracted, remember that the sum difference rule also works when functions are added.
Product rule
Assume you have two functions, u = g(x) and v = h(x). Further, assume that y = u × v.
The derivative of y with respect to x equals the sum of u multiplied by the derivative of v and v multiplied by the derivative of u, or if
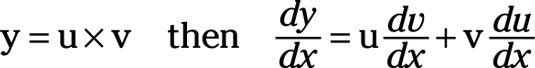
For example, if
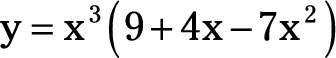
In this equation, u = x3 and v = (9 + 4x - 7x2). Thus, the derivative of u with respect to x is
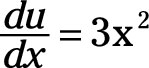
And the derivative of v with respect to x is
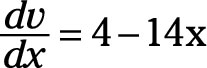
Then
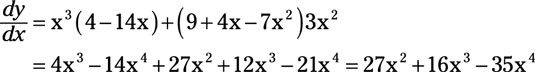
Quotient rule
A quotient refers to the result obtained when one quantity, in the numerator, is divided by another quantity, in the denominator.
Assume you have two functions, u = g(x) and v = h(x). So, u is the quantity in the numerator, and it’s a function g of x. And v is the quantity in the denominator, and it’s a different function of x as represented by h. In addition, assume that y = u/v. So y is the quotient of u divided by v.
The derivative of y with respect to x has two components in its numerator. The first component is the original equation for v multiplied by the derivative of u taken with respect to x, du/dx. From that amount, you subtract the numerator’s second component, the original equation u multiplied by the derivative of v taken with respect to x, dv/dx.
The dominator of this derivative is simply the original equation, v, squared. Thus,
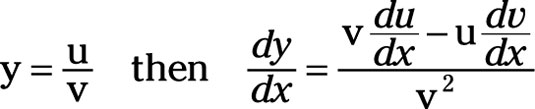
For example, if the original quotient is
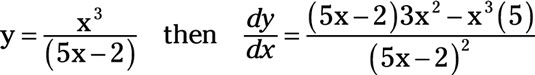
In this quotient, u = x3 and v = (5x - 2). The derivative of u with respect x is
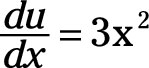
And the derivative of v with respect to x is
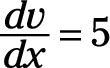
Thus, the first component of the numerator is v multiplied du/dx. From that, you subtract the second component of the numerator, which is u multiplied by dv/dx, or
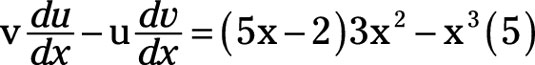
The denominator is v2 or
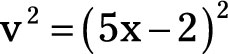
Substituting everything into the quotient rule yields
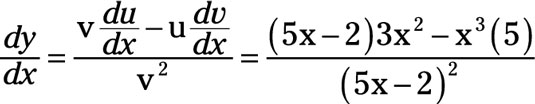
Chain rule
You’re almost there, and you’re probably thinking, “Not a moment too soon.” Just one more rule is typically used in managerial economics — the chain rule.
For the chain rule, you assume that a variable z is a function of y; that is, z = f(y). In addition, assume that y is a function of x; that is, y = g(x). The derivative of z with respect to x equals the derivative of z with respect to y multiplied by the derivative of y with respect to x, or
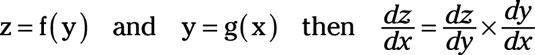
For example, if
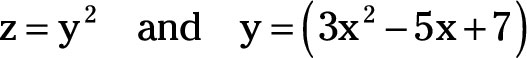
Then
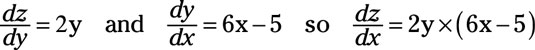
Substituting y = (3x2 – 5x +7) into dz/dx yields
With this last substitution, you remove the third variable y from the derivative, and as a result, you have a function for dz/dx only in terms of x.






