When investigating the effect of a price change, a good place to start is by thinking about what the change will do to the behavior of a representative consumer. Indifference curves excel in this situation!
Start at a given equilibrium to get a sense of what is happening before you make changes. In this case, the plot shown is an equilibrium with well-behaved indifference curves and a standard budget constraint, and at the consumer optimum, the price ratio equals the marginal rate of substitution between goods x1 and x2.
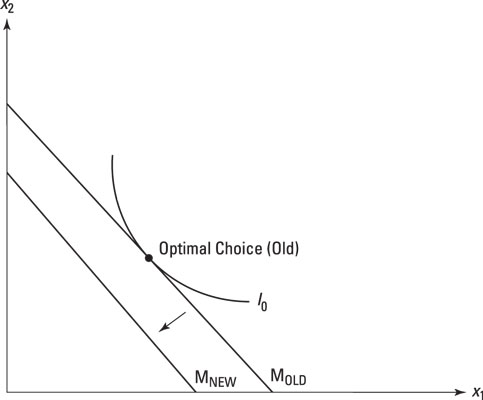
Now, imagine some situation that affects your income calamitously (such as losing your job, getting a new job that doesn't pay as much, or a national economic disaster like that affecting Greece). The details don't matter; the important thing is that it reduces your income.
Starting at the equilibrium, you can draw in a new budget constraint, one that's parallel to the original one, but to the left of it. Of course, this means that the original equilibrium level of utility is now unattainable, and so you, as the representative consumer, react by reducing your consumption of goods x1 and x2. The parallel shift makes the old optimal choice unavailable, given the new constraint MNEW.
Suppose instead that just one price changes (remember, you can treat x1 and x2 as though x1 is the good you're interested in and x2 represents all other goods). This is an interesting situation, because the effect on your purchasing opportunities isn't due to an overall fall in income, but to the relative price effect whereby x1 is now more expensive relative to the price of all other goods available. This situation is where indifference curves fully unpack their awesome power.






