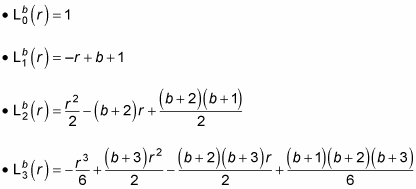If your quantum physics instructor asks you to find the wave function of a hydrogen atom, you can start with the radial Schrödinger equation, Rnl(r), which tells you that
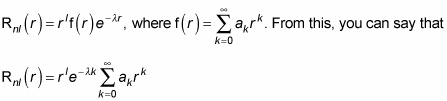
The preceding equation comes from solving the radial Schrödinger equation:
The solution is only good to a multiplicative constant, so you add such a constant, Anl (which turns out to depend on the principal quantum number n and the angular momentum quantum number l), like this:
You find Anl by normalizing Rnl(r).
Now try to solve for Rnl(r) by just flat-out doing the math. For example, try to find R10(r). In this case, n = 1 and l = 0. Then, because N + l + 1 = n, you have N = n – l – 1. So N = 0 here. That makes Rnl(r) look like this:
And the summation in this equation is equal to
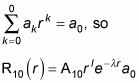
And because l = 0, rl = 1, so
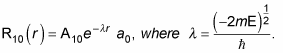
Therefore, you can also write
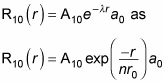
where r0 is the Bohr radius. To find A10 and a0, you normalize
to 1, which means integrating
over all space and setting the result to 1.
and integrating the spherical harmonics, such as Y00, over a complete sphere,
gives you 1. Therefore, you’re left with the radial part to normalize:
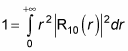
Plugging
into
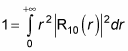
gives you
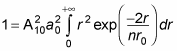
You can solve this kind of integral with the following relation:
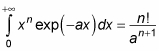
With this relation, the equation
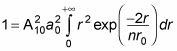
becomes
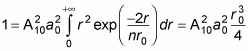
Therefore,
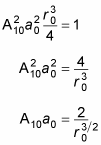
This is a fairly simple result. Because A10 is just there to normalize the result, you can set A10 to 1 (this wouldn’t be the case if
involved multiple terms). Therefore,
That’s fine, and it makes R10(r), which is
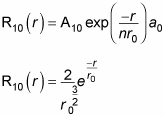
You know that
And so
becomes
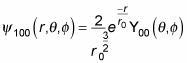
Whew. In general, here’s what the wave function
looks like for hydrogen:
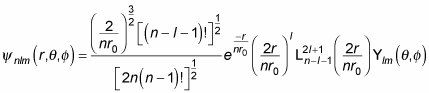
where
is a generalized Laguerre polynomial. Here are the first few generalized Laguerre polynomials: