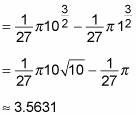The nice thing about finding the area of a surface of revolution is that there’s a formula you can use. Memorize it and you’re halfway done.
To find the area of a surface of revolution between a and b, watch this video tutorial or follow the steps below:
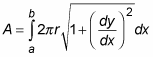
This formula looks long and complicated, but it makes more sense when you spend a minute thinking about it. The integral is made from two pieces:
The arc-length formula, which measures the length along the surface
The formula for the circumference of a circle, which measures the length around the surface
So multiplying these two pieces together is similar to multiplying length and width to find the area of a rectangle. In effect, the formula allows you to measure surface area as an infinite number of little rectangles.
When you’re measuring the surface of revolution of a function f(x) around the x-axis, substitute r = f(x) into the formula:
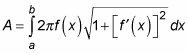
For example, suppose that you want to find the area of revolution that’s shown in this figure.
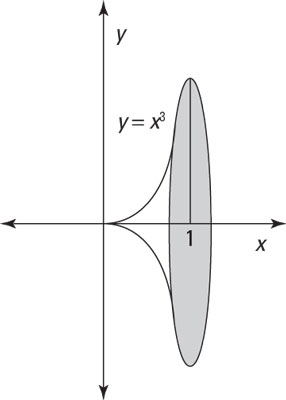
To solve this problem, first note that for
So set up the problem as follows:
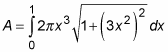
To start off, simplify the problem a bit:
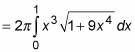
You can solve this problem by using the following variable substitution:
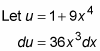
Now substitute u for 1+ 9x4 and
for x3 dx into the equation:
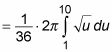
Notice that you change the limits of integration: When x = 0, u = 1. And when x = 1, u = 10.
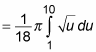
Now you can perform the integration:
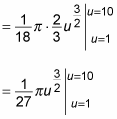
Finally, evaluate the definite integral: