At some point, your quantum physics instructor may want you to find the total energy equation for three-dimensional free particle problems. The total energy of the free particle is the sum of the energy in three dimensions:
E = Ex + Ey + Ez
With a free particle, the energy of the x component of the wave function is
And this equation works the same way for the y and z components, so here’s the total energy of the particle:
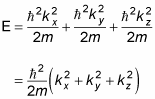
Note that kx2 + ky2 + kz2 is the square of the magnitude of k — that is,
Therefore, you can write the equation for the total energy as
Note that because E is a constant, no matter where the particle is pointed, all the eigenfunctions of
are infinitely degenerate as you vary kx, ky, and kz.






