If you can break up a product of trig functions into the sum of two different terms, each with its own trig function, doing the math becomes much easier. In pre-calculus, problems of this type usually say "express the product as a sum or difference." In the following example, you'll make the conversion from a product to a sum.
You have three product-to-sum formulas to digest: sine multiplied by cosine, cosine multiplied by cosine, and sine multiplied by sine.
Suppose that you're asked to express 6 cos q sin 2q as a sum. Rewrite this expression as 6 sin 2q cos q (thanks to the commutative property) and then plug what you know into the formula to get
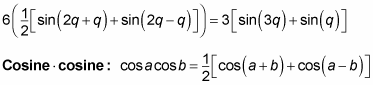
For example, to express
as a sum, rewrite it as the following:
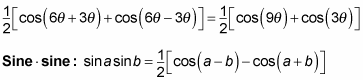
To express sin 5x cos 4x as a sum, rewrite it as the following:






