How to Find a Common Denominator of a Fraction to Solve a Trig Identity

Fractions are your friends. You may not believe this now, but the more you work with trigonometry functions, the more you’ll like fractions. Finding a common denominator to combine fractions often paves the way to solving an identity.

In the identity

the two denominators on the left have nothing in common, so you multiply each fraction by the other’s denominator — or, rather, by that denominator over itself, which equals 1.

1. Multiply each fraction on the left by an equivalent of 1 to create a common denominator.

   

2. Multiply the fractions together and simplify the numerators.

   Leave the denominator alone.

   

3. Replace the first numerator with its equivalent by using the Pythagorean identity.

   The fractions are opposites of one another.

   

Now, prove the identity

by finding a common denominator.

1. Multiply each fraction on the left by the equivalent of 1, creating a common denominator.

   

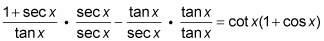
2. Simplify the numerators by multiplying out the fractions.

   

3. Replace tan²x with its equivalent by using the Pythagorean identity.

   Then combine the two numerators.

   

4. Simplify the numerator.

   Then rewrite the left side as the product of two fractions. You have to carefully select where to put the numerator — to your best advantage.

   

5. Multiply the fraction with sec x in the denominator by cos x divided by cos x, which is equivalent to 1.

   

6. Multiply out the second fraction, distributing through the numerator.

   

   Because cos x and sec x are reciprocals, their product is 1.

7. Substitute 1 in both the numerator and the denominator.

   

8. Replace the reciprocal of tan x with cot x.